Chaos, fractals, and Arcadia

Chaos, Fractals, and Arcadia

The Sierpinski Hexagon

As another example of Thomasina's algorithm, start with six points arranged at the vertices of a hexagon. Number them from one to six and erase the colors on your die. Beginning with an initial seed in the hexagon, roll the die and then move the point two-thirds of the distance toward the appropriate vertex. Then iterate this procedure. As before, do not record the first 15 or so iterations, but plot the rest. The result is again anything but a random mess: It is the Sierpinski hexagon. See Figure 3.

Fig. 3. The Sierpinski hexagon.

Note that these two fractal images are not quite the lifelike images that Thomasina promised us, but there is a hint of what is to come. Look at the innermost boundary of the Sierpinski hexagon. Note how it resembles a snowflake. Indeed, this innermost boundary is the Koch snowflake curve, another very famous fractal.

This particular algorithm can also be expressed in terms of linear contractions of a given square. Start with a square and place six points on the square so that they form the boundary of a hexagon with equal sides. Geometry exercise: Where should these points be placed if vertex number one lies in the middle of the left side of the square? At each iteration, contract all points in the original square toward the appropriate vertex. The image is, in each case, a square exactly one-third the size of the original and located as shown in Figure 4.

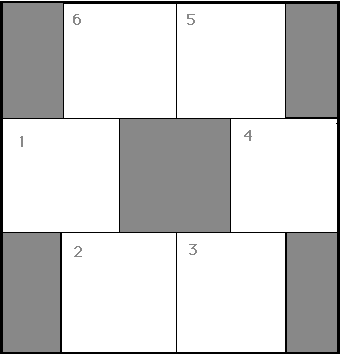
Fig. 4. The six contractions to produce the Sierpinski hexagon.

$next$ Thomasina's Fern (Next Section)

$up$ Table of Contents

(Return to Dynamical Systems and Technology Home Page)