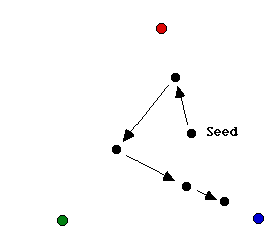
Figure 1: Playing the chaos game with rolls of red, green, blue, blue.
 The Sierpinski
triangle. (Next Section)
The Sierpinski
triangle. (Next Section) Chaos in the Classroom
(Cover Page)
Chaos in the Classroom
(Cover Page) Chaos in the Classroom
(Previous Section)
Chaos in the Classroom
(Previous Section) BU Math Home Page
BU Math Home Page
One of the most interesting fractals arises from what Michael Barnsley has dubbed ``The Chaos Game'' [Barnsley]. The chaos game is played as follows. First pick three points at the vertices of a triangle (any triangle works---right, equilateral, isosceles, whatever). Color one of the vertices red, the second blue, and the third green.
Next, take a die and color two of the faces red, two blue, and two green. Now start with any point in the triangle. This point is the seed for the game. (Actually, the seed can be anywhere in the plane, even miles away from the triangle.) Then roll the die. Depending on what color comes up, move the seed half the distance to the appropriately colored vertex. That is, if red comes up, move the point half the distance to the red vertex. Now erase the original point and begin again, using the result of the previous roll as the seed for the next. That is, roll the die again and move the new point half the distance to the appropriately colored vertex, and then erase the starting point. See Figure 1.

Now continue in this fashion for a small number of rolls of the die. Five rolls are sufficient if you are playing the game ``by hand'' or on a graphing calculator, and eight are sufficient if you are playing on a high-resolution computer screen. (If you start with a point outside the triangle, you will need more of these initial rolls.)
After a few initial rolls of the die, begin to record the track of these traveling points after each roll of the die. The goal of the chaos game is to roll the die many hundreds of times and predict what the resulting pattern of points will be. Most students who are unfamiliar with the game guess that the resulting image will be a random smear of points. Others predict that the points will eventually fill the entire triangle. Both guesses are quite natural, given the random nature of the chaos game. But both guesses are completely wrong. The resulting image is anything but a random smear; with probability one, the points form what mathematicians call the Sierpinski triangle and denote by S (see Figure 2).
A few words about the coloring here is in order. We have used color merely to indicate the proximity of the vertex with the given color. For example, the portion of the triangle closest to the green vertex is colored green, and so forth.
There is some terminology associated with the chaos game that is important. The sequence of points generated by the chaos game is called the orbit of the seed. The process of repeating the rolls of the die and tracing the resulting orbit is called iteration. Iteration is important in many areas of mathematics. In fact, the branch of mathematics known as discrete dynamical systems theory is the study of such iterative processes.
There are two remarkable facets of the chaos game. The first is the geometric intricacy of the resulting figure. The Sierpinski triangle is one of the most basic types of geometric images known as fractals. The second is the fact that this figure results no matter what seed is used to begin the game: With probability one, the orbit of any seed eventually fills out S. The words ``with probability one'' are important here. Obviously, if we always roll ``red,'' the orbit will simply tend directly to the red vertex. Of course, we do not expect a fair die to yield the same two numbers at each roll.
 The Sierpinski triangle. (Next Section)
The Sierpinski triangle. (Next Section) Chaos in the Classroom (Cover Page)
Chaos in the Classroom (Cover Page) Chaos in the Classroom (Previous Section)
Chaos in the Classroom (Previous Section) BU Math Home Page
BU Math Home Page