BU Math Home Page

Fractal Dimension

Students (and teachers) are often fascinated by the fact that certain geometric images have fractional dimension. The Sierpinski triangle provides an easy way to explain why this must be so.

To explain the concept of fractal dimension, it is necessary to understand what we mean by dimension in the first place. Obviously, a line has dimension 1, a plane dimension 2, and a cube dimension 3. But why is this? It is interesting to see students struggle to enunciate why these facts are true. And then: What is the dimension of the Sierpinski triangle?

They often say that a line has dimension 1 because there is only 1 way to move on a line. Similarly, the plane has dimension 2 because there are 2 directions in which to move. Of course, there really are 2 directions in a line -- backward and forward -- and infinitely many in the plane. What the students really are trying to say is there are 2 linearly independent directions in the plane. Of course, they are right. But the notion of linear independence is quite sophisticated and difficult to articulate. Students often say that the plane is two-dimensional because it has ``two dimensions,'' meaning length and width. Similarly, a cube is three-dimensional because it has ``three dimensions,'' length, width, and height. Again, this is a valid notion, though not expressed in particularly rigorous mathematical language.

Another pitfall occurs when trying to determine the dimension of a curve in the plane or in three-dimensional space. An interesting debate occurs when a teacher suggests that these curves are actually one-dimensional. But they have 2 or 3 dimensions, the students object.

So why is a line one-dimensional and the plane two-dimensional? Note that both of these objects are self-similar. We may break a line segment into 4 self-similar intervals, each with the same length, and ecah of which can be magnified by a factor of 4 to yield the original segment. We can also break a line segment into 7 self-similar pieces, each with magnification factor 7, or 20 self-similar pieces with magnification factor 20. In general, we can break a line segment into N self-similar pieces, each with magnification factor N.

A square is different. We can decompose a square into 4 self-similar sub-squares, and the magnification factor here is 2. Alternatively, we can break the square into 9 self-similar pieces with magnification factor 3, or 25 self-similar pieces with magnification factor 5. Clearly, the square may be broken into N^2 self-similar copies of itself, each of which must be magnified by a factor of N to yield the original figure. See Figure 8. Finally, we can decompose a cube into N^3 self-similar pieces, each of which has magnification factor N.

Figure 8: A square may be broken into N^2 self-similar pieces, each with magnification factor N

Now we see an alternative way to specify the dimension of a self-similar object: The dimension is simply the exponent of the number of self-similar pieces with magnification factor N into which the figure may be broken.

So what is the dimension of the Sierpinski triangle? How do we find the exponent in this case? For this, we need logarithms. Note that, for the square, we have N^2 self-similar pieces, each with magnification factor N. So we can write

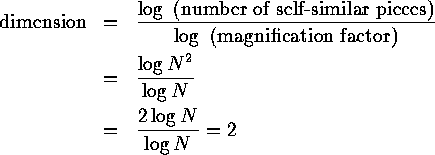
Similarly, the dimension of a cube is

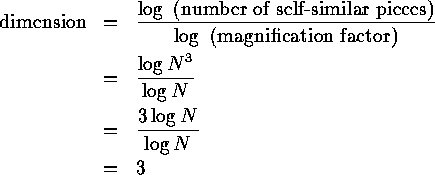
Thus, we take as the definition of the fractal dimension of a self-similar object

Now we can compute the dimension of S. For the Sierpinski triangle consists of 3 self-similar pieces, each with magnification factor 2. So the fractal dimension is

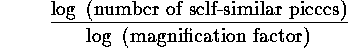
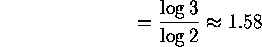
so the dimension of S is somewhere between 1 and 2, just as our ``eye'' is telling us.

But wait a moment, S also consists of 9 self-similar pieces with magnification factor 4. No problem -- we have

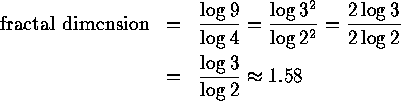
as before. Similarly, S breaks into 3^N self-similar pieces with magnification factors 2^N, so we again have

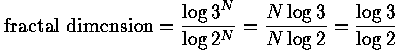
Fractal dimension is a measure of how "complicated" a self-similar figure is. In a rough sense, it measures "how many points" lie in a given set. A plane is "larger" than a line, while S sits somewhere in between these two sets.

On the other hand, all three of these sets have the same number of points in the sense that each set is uncountable. Somehow, though, fractal dimension captures the notion of "how large a set is" quite nicely, as we will see below.

BU Math Home Page