Exploration #1


|
Question: What is the Mandelbrot set?
Answer: The Mandelbrot set is a picture in the complex
"c-plane" of the fate of the orbit
of 0
under iteration of the
function x2 + c. A c-value is in the Mandelbrot set
if the orbit of 0 under iteration of x2 + c for the
particular value of c does not tend to infinity. If the orbit of 0
tends to infinity, then that c-value is not in the Mandelbrot set.
|

|
Question: Hey man, slow down! Wanna give me that in English?
(please...)
Answer: OK, here we go again. You give me a complex number,
call it c. Then I will tell you whether c is in the
Mandelbrot set. OK? Here's how I do it. I start with the function
x2 + c. Then I take 0 and put it into the
function. That is, I
compute 02 + c which gives c. Then I do
this again, using the output from the previous computation as the
input for the next. That is,
I now use c and compute c2 + c.
Then I do it again: I get (c2 + c)2 +
c. And so forth. I generate a list of complex numbers in this
way. If these complex numbers (called the orbit of 0) get
larger and
larger (or further and further away from the origin), then your
choice of c is NOT in the Mandelbrot set. But if this is not
the case (the orbit stays "bounded"), then c IS in the
Mandelbrot set. Are you happy now?
|
In each of the following five examples, observe the following
information:
- The location of c in or around the Mandelbrot set.
- The list of the first few points on the orbit of 0.
- The location of this orbit in the complex plane.
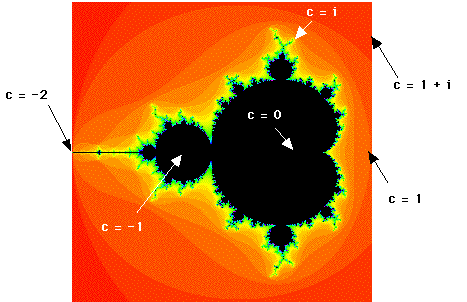
Example 1: c = 0 .
Example 2: c = -1 .
Example 3: c = i .
Example 4: c = - 2 .
Example 5: c = 2 i .
Question 1A: Is c = 3 in the Mandelbrot set? Answer
Question 1B: Is c = 1 in the Mandelbrot set? Answer
Question 1C: Is c = 1 + i in the Mandelbrot set? Answer
Thus we see that the following c-values are in the Mandelbrot
set:
- c = 0
- c = i
- c = -2
- c = -1
whereas the following c-values are not in the Mandelbrot set:
- c = 2i
- c = 3
- c = 1
- c = 1 + i
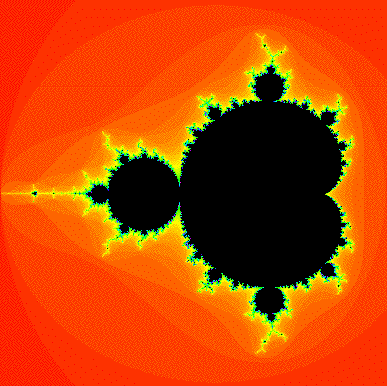
We may therefore begin to "paint" the picture of the Mandelbrot set by
coloring complex numbers in the c-plane according to the
following rule:
- Color a c-value black if c lies in the Mandelbrot
set (that is, the corresponding orbit of c does not escape to
infinity.
- Color a c-value a different color if the orbit escapes to
infinity. In the Explorer, we always use the following algorithm to
color points: red points escape fastest.
That is, it takes very few iterations for the orbit of 0 under
iteration of x2 + c to
become far from the origin. Red points are
followed in order by orange,
yellow,
green,
blue,
indigo,
and violet. That is we use the colors
drawn from the light spectrum for points that are not in the
Mandelbrot set. The important thing is: red
points escape fastest, while violet
points take the most iterations to go far away from the origin.
Thus we have the following picture so far:
Further Exploration:
The Java applet below allows you to click on a point in or around the
Mandelbrot set and then view the fate of the orbit of 0. By fate of
the orbit we mean the eventual behavior of the orbit of 0: We do not
plot all of the points on the orbit of 0. We merely display the
points number 25, 26, 27, etc. on the orbit of 0.
- In many cases the
orbit of 0 tends to a cycle of period
n.
In this case we display that
cycle as well as its period.
- Sometimes the orbit of 0 does not tend to a cycle or tends to a
cycle with an extremely
large period that we cannot compute in a reasonable
amount of time.
In this case we report the fate of the
orbit as "cannot determine period."
- If the orbit tends to infinity, we report "goes to infinity" and
do not plot the orbit.
Please note that your browser must be Java-enabled in order to use
this applet. All recent versions of Netsapce or Internet Explorer are
Java-enabled.



For Further Information:
 Devaney home page
Devaney home page
 Dynamical Systems and Technology Project
Home Page
Dynamical Systems and Technology Project
Home Page


Dynamical Systems and Technology Project
Home Page