Question: How do you find the rotation number of the largest bulb that lies between two given adjacent, even larger primary bulbs? Answer: Amazingly, given two primary bulbs with no larger bulbs in between, you can find the rotation number of the largest bulb in between by adding the fractions "just the way you always wanted to add fractions" --- namely by adding the numerators and the denominators. Please do not do this in your math class... it's illegal everywhere except here!

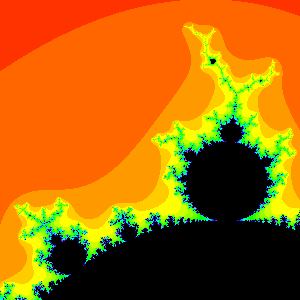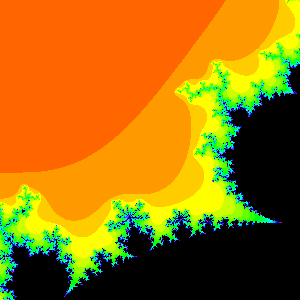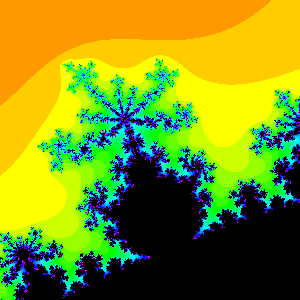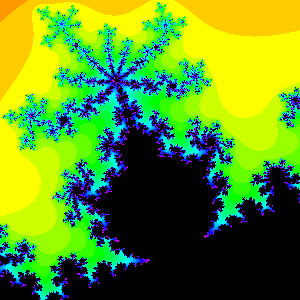
Example 1: In this figure you see the 2/5 bulb in the lower left and the 1/3 bulb in the upper right. The largest bulb in between is magnified: note that it is the 3/8 bulb. And if we add 2/5 and 1/3 the wrong way we get: (2 + 1) / (5 + 3) = 3/ 8. Weird, huh?

Example 2: Here is another example. The largest visible bulbs in this magnification of the Mandelbrot set are the 2/5 bulb on the left and the 3/8 bulb on the right. In between sits the largest bulb which has rotation number 5/13. And again, (2 + 3) / (5 + 8) = 5 / 13. Isn't this great? But remember, if you ever do this in math class, you'll be in BIG trouble!

Exploration: Do you see the omnipresent Fibonacci sequence in the Mandelbrot set? As a hint, click here. Warning: This file is large --- 8 Mb --- and will take a while to download.

For Further Information: See the papers:

• The Fractal Geometry of the Mandelbrot Set. II: How to Add and How to Count. Robert L. Devaney. Accessible to high school students with a solid background in complex numbers.

• The Mandelbrot and Julia Sets: A Toolkit of Dynamics Activities. Robert L. Devaney. Pages 105-114. Key Curriculum Press. Accessible to advanced high school students.

• The Mandelbrot Set and the Farey Tree. Robert L. Devaney. Postscript File. Amer. Math. Monthly 106 (1999), 289-302. Accessible to advanced math majors in college.

• Geometry of the Antennas in the Mandelbrot Set. Postscript File. Robert L. Devaney and Monica Moreno Rocha. In the journal Fractals. 10 (2002), 39-46. For graduate students in Mathematics.

Devaney home page

Dynamical Systems and Technology Project Home Page