MA 226:
Ordinary Differential Equations
Sample Exam 2
Do all problems and show all work.
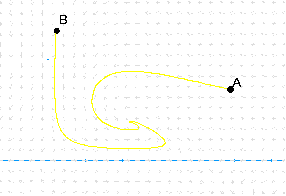
1. Consider the predator prey system
R' = 2R(1 - 0.5R) -1.2 RF
F' = -F + 0.9 RF.
Here is the phase plane for this system with two solution curves
sketched.
First indicate the approximate locations of all equilibrium solutions
on this picture.
Then, for each of the solution curves A and B, draw the corresponding
x(t) and y(t) graphs.
2. We have not covered all of the
material relevant to this question yet.
Consider the system of differential equations
x' = x(-x - 3y +150)
y' = y(-2x -y + 100)
- Draw the x- and y- nullclines for this system.
- Find all equilibrium points for this system and
sketch their locations on your picture of the nullclines.
- Indicate by little arrows the direction of the vector field
in all regions bounded by the nullclines.
- What can you say about the fate of the solution curve beginning
at (60, 20)? Sketch this solution curve.
- What about the fate of the solution beginning at
(20, 20)? What are the possible fates for this
solution?
3. Consider the linear system
x' = -4x + y
y' = 2x - 3y
- Find the eigenvalues and eigenvectors of the associated
coefficient matrix.
- Write down the general solution of this system.
- Solve the initial value problem Y(0) = (1, 1).
- Sketch this solution curve in the phase plane.
- Also sketch the and y(t) graphs.
4. In an essay, discuss the different kind of phase plane pictures
that can occur for constant coefficient linear systems of the form
x' = ax + by
y' = cx + dy
when the eigenvalues of the system are real (and distinct).
Be sure to include pictures of typical types of systems and discuss
the eigenvalues corresponding to each type.
5. Consider the second order equation for a harmonic oscillator
y'' + y' + 4y = 0.
- Write this equation in system form
- Solve the initial value problem y(0)=2, y'(0) = 0.
- In a brief paragraph, describe the motion of the mass
corresponding to this solution.
- Sketch the graph of y(t).
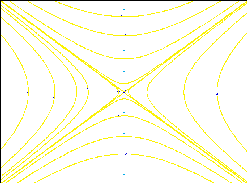
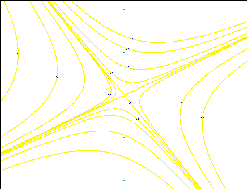
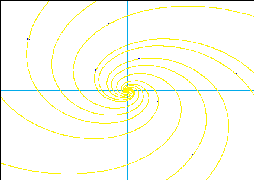
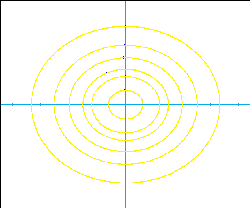
6. Here are four phase planes and four systems. Match them.
A.
x' = 2y, y' = -2x
B.
x' = 2y, y' = 2x
C.
x' = x+2y, y' = 2x-y
D.
x' = x+2y, y' = -2x + y
7. Show that, for the linear system Y' = AY, if AV = kV for
some nonzero vector V, then
Y(t) = ektV
is a solution of the system.
MA226 Main Menu