MA 226: Lab 2

Two Parameter Families of Differential Equations

This lab is due Thursday, October 26, 2017 in class. No late labs or electronic versions can be accepted.

Please write your name and discussion section day and time on the first page.

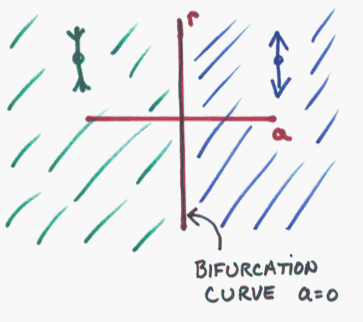
In this lab you will investigate three families of first order differential equations that each depend on two parameters, a and r. The goal in each case is to give a sketch of the "bifurcation plane" (or "parameter plane"). The bifurcation plane is a picture in the a,r-plane of the regions (i.e., the values of a and r) for which there are different types of phase lines (specifically, different numbers of equilibria). The curves that separate these regions are the parameters where bifurcations occur (the "bifurcation curve"). For the first two families, first find all of the equilibrium points and determine their types (these equilibria will, of course, depend on a and r). Then sketch the bifurcation curve(s) and the regions in the a,r-plane where you find different numbers of equilibrium points, and, in each different region, draw a representative picture of the phase line for any a and r value in this region. Finally, describe in a sentence or two the bifurcations that occur as you move from each region to an adjacent region. An example of what is expected in this lab is below for the family y' = r + ay

Family #1. y' = r + ay - y²     Hint: You can use the Phase Lines tool to help out on this one.

Family #2. y' = ry + ay²

For the final example, you need not find the equilibrium points, their types, and the formulas for the curves in the bifurcation plane that separate these regions. Rather, just use the Phase Lines tool to view the graphs, phase lines, and bifurcation diagrams for the following family. Then use these pictures to give an approximate sketch of the bifurcation plane with the corresponding phase lines included.

Family #3. y' = r + ay - y³

Example: Bifurcation diagram for y' = r + ay

The equilibrium points are given by y = -r/a. So we have

• Only one equilibrium point if a is non-zero. This equilibrium point is a source if a > 0 and a sink if a < 0.
• No equilibrium points if a = 0 and r is non-zero
• All points on the phase line are equilibria if r = a = 0.

So a bifurcation occurs as a passes through 0. There are three possible ways this can occur:

• If this happens at a point in the bifurcation plane of the form (0, r) with r > 0, then what happens is the equilibrium point moves off to positive infinity when a approaches 0 from the negative side and then reappears near negative infinity when a is positive. When a = 0, all solutions increase from negative to positive infinity.
• If this happens at a point in the bifurcation plane of the form (0, r) with r < 0, then the equilibrium point moves off to negative infinity as a approaches 0 from the negative side and it reappears near positive infinity when a is positive. When a = 0, all solutions decrease from positive to negative infinity.
• If the bifurcation occurs as the parameter passes through (0,0), then we always have a single equilibrium point when a is non-zero, but when a = 0, suddenly every point is an equilibrium point.

The bifurcation plane picture is: