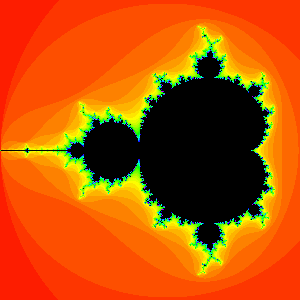
The aim of this course is to introduce mathematicians to current research in complex dynamics. We will begin with an overview of the classical work of Julia and Fatou on the dynamics of complex analytic maps. Much of the course will be devoted to the study of the dynamics of complex transcendental functions. The main goal will be to understand in depth the dynamics of quadratic functions and the geometry of the Mandelbrot set, followed by the very different dynamics of the complex exponential.

This course is a graduate level seminar aimed at graduate students in mathematics. Prerequisites include a background in discrete dynamical systems (at the level of MA 771 at Boston University) and a graduate level course in complex analysis (at the level of MA 713). Students should be familiar with the following topics from dynamics: iteration, local behavior near periodic points, chaotic behavior, symbolic dynamics, and some elementary bifurcation theory. From complex analysis, students should know the Riemann mapping theorem, Schwarz Lemma, and properties of analytic mappings.

Students who register for the course will be required to make several presentations during the course on a topic of current interest in the literature.

There is no textbook for the course. Lectures will be drawn mainly from the research literature. Some background sources include:

• Alexander, Daniel S. A History of Complex Dynamics Vieweg, 1994.
• Carleson, L. and Gamelin, T. W. Complex Dynamics.
• Devaney, R. L. An Introduction to Chaotic Dynamical Systems, Perseus Press (Westview Press) (chapter 3 only).
• McMullen, C. Complex Dynamics and Renormalization, Princeton University Press.
• Milnor, J. Dynamics in One Complex Variable, Vieweg.

Topics to be covered include: