Gennady Samorodnitsky
Murad S. Taqqu
 -stable self-similar processes
with stationary increments and
a ``moving average'' representation. The
representation involves two real parameters a and b. When
-stable self-similar processes
with stationary increments and
a ``moving average'' representation. The
representation involves two real parameters a and b. When 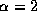 ,
the processes are identical to the Gaussian Fractional Brownian motion for all
values of a and b. We will
show that different values of the parameters a and b yield different
processes when
,
the processes are identical to the Gaussian Fractional Brownian motion for all
values of a and b. We will
show that different values of the parameters a and b yield different
processes when 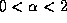 and when the skewness intensity is not
necessarily zero.
and when the skewness intensity is not
necessarily zero.