Non-linear regression of stable random variables

Clyde D. Hardin Jr.
Gennady Samorodnitsky
Murad S. Taqqu

Abstract:

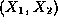Let be an -stable random vector, not necessarily symmetric, with 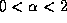. The paper investigates the regression 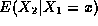for all values of . We give conditions for the existence of the conditional moment 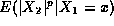when 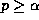, and we obtain an explicit form of the regression 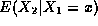as a function of x. Although this regression is, in general, not linear, it can be linear even when the vector 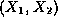is skewed. We give a necessary and sufficient condition for linearity and characterize the asymptotic behavior of the regression as . 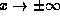The behavior of the regression functions is also illustrated graphically.