56
<P ALIGN=RIGHT><FONT SIZE=+4>56</FONT><P>
A. Astrauskas
Joshua B. Levy
Murad S. Taqqu
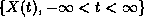 be the linear fractional Lévy motion,
that is, an
be the linear fractional Lévy motion,
that is, an  -stable H-self-similar process with stationary increments,
parametrized by
-stable H-self-similar process with stationary increments,
parametrized by 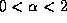 and 0<H<1,
and 0<H<1, 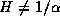 , and possessing a moving-average type representation. Let
, and possessing a moving-average type representation. Let 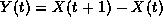 be the increment
process. The asymptotic dependence structure of the stationary process
be the increment
process. The asymptotic dependence structure of the stationary process 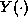 can be measured
for real
can be measured
for real 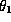 and
and 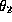 by
by 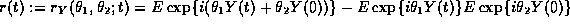 , as
, as 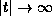 .
It is shown that
.
It is shown that 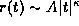 ,
, 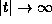 , where
, where 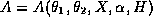 and
and 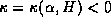 . For example, if
. For example, if 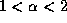 , then
, then 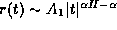 if
if 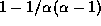 <H<1,
<H<1, 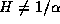 but
but 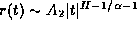 if
if 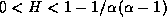 . These results extend initial work of Astrauskas (1984).
The behavior of
. These results extend initial work of Astrauskas (1984).
The behavior of 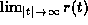 is also studied for the
stationary increments of Log-fractional Lévy motion, an
is also studied for the
stationary increments of Log-fractional Lévy motion, an  -stable
-stable
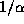 -self-similar process defined for
-self-similar process defined for 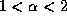 .
.