Continuous functions whose level sets are orthogonal to all polynomials of a given degree

Herold Dehling
Murad S. Taqqu

Abstract:

Let be any continuous non-negative weight function on R with 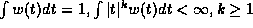. We prove the existence of continuous functions 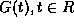for which the indicator functions of the level sets 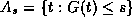with their mean 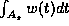subtracted are orthogonal to all polynomials of degree less than or equal to k. The result is used to settle an open problem on empirical processes of long-range dependent sequences.