Weak convergence of sums of moving averages in the alpha-stable domain of attraction

Florin Avram
Murad S. Taqqu

Abstract:

Skorohod has shown that the convergence of sums of i.i.d random variables to an -stable Lévy motion, with 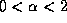, holds in the weak-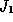 sense. 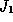is the commonly used Skorohod topology. We show that for sums of moving averages with at least two non-zero coefficients, weak-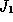 convergence cannot hold because adjacent jumps of the process can coalesce in the limit; however, if the moving average coefficients are positive, then the adjacent jumps are essentially monotone and one can have weak-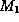 convergence. 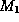is weaker than 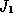, but it is strong enough for the sup and inf functionals to be continuous.