Asymptotic dependence of moving average type self-similar stable random fields

Piotr S. Kokoszka
Murad S. Taqqu

Abstract:

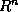We investigate the asymptotic dependence structure of a large class of self-similar stable random fields which are extensions of the linear fractional Lévy motion to the parameter space . The dependence is measured through the difference of the joint characteristic function and the product of the marginal characteristic functions. We show that the intensity of the dependence decreases to zero like a power function as the lag tends to infinity and we obtain the exact expression for the exponent in the power function. The exponent depends on both the stability parameter and the self-similarity parameter.