New classes of self-similar symmetric stable random fields

Piotr S. Kokoszka
Murad S. Taqqu

Abstract:

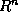We construct two new classes of symmetric stable self-similar random fields with stationary increments, one of the moving average type, the other of the harmonizable type. The fields are defined through an integral representation whose kernel involves a norm on . We examine how the choice of the norm affects the finite-dimensional distributions. We also study the processes which are obtained by projecting the random fields on a one-dimensioanl subspace. We compare these `projection processes' with each other and with other well-known self-similar processes and we characterize their asymptotic dependence structure.