85

<P ALIGN=RIGHT><FONT SIZE=+4>85</FONT><P>

A class of cylindrical pulse processes

Renata Cioczek-Georges
Benoit B. Mandelbrot
Gennady Samorodnitsky
Murad S. Taqqu

Abstract:

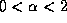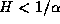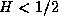A class of -stable, , processes is obtained as a sum of ``up-and-down'' pulses determined by an appropriate Poisson random measure. Processes are H-self-affine (also frequently called ``self-similar'') with and have stationary increments. Their two-dimensional dependence structure resembles that of the fractional Brownian motion (for ), but their sample paths are highly irregular (nowhere bounded with probability 1). Generalizations using different shapes of pulses are also discussed.