1 School of Biomedical Sciences, The Worsley Building, University of Leeds, LS2 9NL, UK.

2 Division of Neuroscience, The Medical School, University of Birmingham, Birmingham B15 2TT, UK.

3 Dept. of Mathematics, Boston University, Boston MA 02215, USA

4 Dept. of Mathematics, University of Pittsburg, Pittsburg PA 15260, USA

Keywords: GABA, inhibition, gamma oscillation, beta oscillation, synchrony, network dynamics

Address as above

tel: +44 113 233 4247

e-mail: m.whittington@leeds.ac.uk

An increasingly large body of data exists which demonstrates that oscillations of frequency 12 - 80 Hz are a consequence of, or are inextricably linked to, the behaviour of inhibitory interneurons in the central nervous system. This frequency range covers the EEG bands beta 1 (12 - 20 Hz), beta 2 (20 - 30 Hz) and gamma (30 - 80 Hz). The pharmacological profile of both spontaneous and sensory-evoked EEG potentials reveals a very strong influence on these rhythms by drugs which have direct effects on GABA_A receptor mediated synaptic transmission (general anaesthetics, sedative/hypnotics) or indirect effects on inhibitory neuronal function (opiates, ketamine). In addition, a number of experimental models of, in particular, gamma-frequency oscillations, have revealed both common denominators for oscillation generation and function, and subtle differences in network dynamics between the different frequency ranges. Powerful computer and mathematical modelling techniques based around both clinical and experimental observations have recently provided invaluable insight into the behaviour of large networks of interconnected neurons. In particular, the mechanistic profile of oscillations generated as an emergent property of such networks, and the mathematical derivation of this complex phenomenon have much to contribute to our understanding of how and why neurons oscillate. This review will provide the reader with a brief outline of the basic properties of inhibition-based oscillations in the CNS by combining research from laboratory models, large-scale neuronal network simulations, and mathematical analysis.

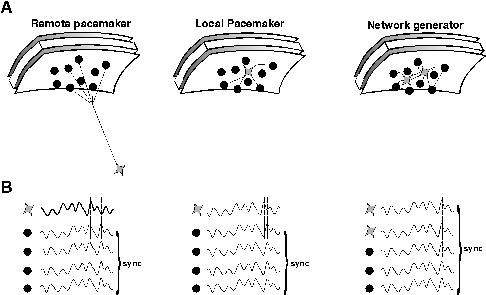
EEG oscillations represent a remote consequence of repetitive, periodic activity in major cell types in the area of brain between recording electrodes and/or a reference electrode. The recorded activity is most likely to originate from activity of populations of excitatory cells in neocortex but is influenced by factors such as the depth and orientation of the cell populations involved. Different types of EEG activity may coexist with different types of electromagnetic field (eg see Tallon Baudry et al., 1997). To be of sufficient magnitude this activity has to be manifest in a large number of neurons proximal to the electrode or, more precisely, in a large enough proportion of the neurons proximal to the electrode, to generate a signal distinct from background noise. This implies a degree of synchronisation, at least locally, of pyramidal cell outputs. There are at least two distinct mechanisms by which such local synchrony can occurr (see fig. 1).

Figure 1

1) Synchrony can be a consequence of a common input. This can be either remote from the area of cortex being recorded or within it. Remote sources of synchronising oscillatory cortical input have been reported in the thalamus. In particular diffuse projection neurons in intralaminar nuclei display gamma band oscillatory activity (Steriade et al., 1993) and high-intensity stimulation of nucleus reticularis neurons generates gamma oscillations in neocortex (MacDonald et al., 1998). Sources of oscillations from local pacemakers in the neocortex include subclasses of pyramidal neurons (Gray & McCormick, 1996).

2) Synchrony can also be a consequence of an emergent population oscillation within the network of cells under the electrode. In this latter case no single neuron within the network acts as a pacemaker. Instead it is the properties of the network as a whole which generate the oscillation observed. Examples of emergent network oscillations in hippocampus and neocortex show a strong dependence on the activity of inhibitory interneurons within the oscillating area (Sik et al., 1995; Whittington et al., 1995; Fisahn et al., 1998; Buhl et al., 1998).Though many other factors may also be involved these oscillations all collapse (at gamma and beta frequencies) in the absence of inhibitory neuronal activity. As we will discuss below, these rhythms are tightly tied to inhibition in both their frequency and ability to form a coherent rhythm. They are therefore referred to as inhibition-based rhythms.

2. Models of inhibition-based rhythms.

There are a number of useful models available to examine the dynamics of oscillations as an emergent property of neuronal networks. The basic ingredients of the models are highlighted below, but in general each consists of an in vitro brain slice preparation in which an area of hippocampus or neocortex is maintained in a tissue chamber and induced to oscillate via electrical stimulation or exogenous drug application.

i). The first demonstration of a network oscillator generating gamma frequency oscillations in both hippocampal area CA1 and superficial regions of the neocortex was published in 1995 (Whittington et al., 1995). The model consists of tonic activation of both interneurons and pyramidal cells in a small area of brain via exogenous application of a specific metabotropic glutamate receptor (mGluR) agonist or glutamate itself in the presence of antagonists of ionotropic glutamate receptors. Activation of mGluRs with agonists such as ACPD (Whittington et al., 1995; Traub et al., 1996) or the group 1 metabotropic glutamate receptor agonist DHPG (Fisahn et al., 1998) generates a long-lasting (several seconds to hours) depolarisation of both excitatory and inhibitory cells within the region exposed to the drug. Superimposed on this depolarisation is a train of inhibitory postsynaptic potentials present, again, in both cell types.

In the presence of ionotropic (ie NMDA and AMPA) glutamate receptor blockers, the nature of the inhibitory oscillation produced can be analysed in isolation, without interference from fast excitatory inputs onto interneurons from local excitatory cells. This situation has proved useful for studying the dynamics of inhibitory network oscillations but may be seen as an artificial situation, where drugs effectively uncouple the interneuron network from fast excitatory influences. However, there may be physiological correlates when examining the afferent input to auditory cortex from subcortical areas (Barth & MacDonald, 1996), or tonic excitation of populations of purely inhibitory neurons such as the thalamic reticular nucleus (Pinault & Deschênes, 1992).

ii) Using similar experimental techniques to i) above, in the absence of ionotropic glutamate blockade, a model of network oscillations which maintains all fast excitatory connections between neurons can be produced. In this situation, one can analyse the effects of a tonically activated area on the behaviour of a (possibly distinct) oscillating area, and the response to both excitatory and inhibitory input can be quantified (Burchell et al., 1998). As with the isolated inhibitory network model above, the drug used to generate the long-lasting drive needed to expose the oscillatory activity has to be applied briefly. This is usually done using pressure ejection of a small volume of glutamate or specific mGluR agonist from a pipette placed within the area to be activated. Rapidly repeated application of glutamate produces desensitisation of the oscillatory response - something not seen with the metabotropic cholinergic model (see below).

iii) Electrical stimulation of a brain region directly or stimulation of major afferent input fibers can also generate gamma oscillations (Traub et al., 1996a). The form of stimulation is usually that of a tetanus consisting of 8 - 20 pulses given at 100 Hz. The shorter duration tetani resemble sharp waves seen in hippocampus and entorhinal cortex (Buzsáki, 1986). Tetani have also been used successfully to study thalamocortical gamma oscillations (MacDonald et al., 1998). Such stimulation produces a post-tetanic depolarisation, superimposed on which is a gamma oscillation taking the form of trains of GABA_A receptor-mediated inhibitory synaptic events. Similar post-spike train gamma oscillations are seen following the hippocampal sharp wave and after burst discharges generted by 4-AP or low extracellular magnesium ions (in the neocortex) (Traub et al., 1996b; Antkowiack & Hentsche, 1998; Funahashi & Stewart, 1998).

The sources of the depolarisation underlying such activity-induced gamma are more diverse than with direct activation of metabotropic glutamate receptors. Though mGluRs still generate the majority of the depolarisation there is also a marked NMDA receptor-mediated component as well (Whittington et al., 1997). These two facets of glutamatergic neurotransmission have been shown to work synergistically in generating post-synaptic excitatory responses (Alagarsamy et al., 1999), and may, in part, underlie the plastic changes associated with inhibition based rhythms.Such post-tetanic depolarisations are also associated with some degree of cholinergic excitation (Whittington et al., 1997) which can account, in some conditions, for the entire post-tetanic depolarisation with stratum oriens/alveus tetani (Cole & Nicoll, 1984).

In addition a depolarising GABA component in excitatory pyramidal cells has been seen to predominate in the post-tetanic response by one group (Bracci et al., 1999). This suggests that activation of a network of inhibitory cells to produce an inhibition-based rhythm may be accentuated by the activity of the interneurons themselves, producing a self-sustaining oscillation. However, these authors used conditions which would be expected to accentuate any depolarising GABA component (immature animals, relatively high bicarbonate concentrations extracellularly and plasma pH levels) and demonstrated that, in these conditions, the post-tetanic spike-train consisted of little, if any, measurable fast inhibitory synaptic component.

iv) Carbachol bath application. Superfusion of hippocampal and neocortical slices with the cholinergic agonist carbachol results in the induction of gamma frequency network oscillations (Buhl et al., 1998; Fisahn et al., 1998). In the hippocampus activity originates in the CA3 area and spreads into the CA1 area, since transection of the Schaffer collateral pathway can usually abolish activity in the CA1 area. Oscillations persist for many hours and can be pharmacologically antagonized by atropine, suggesting a major involvement of muscarinic receptors in the induction process. Gamma activity is also susceptible to GABA_A and AMPA/kainate receptor antagonists, suggesting a role of fast IPSPs and EPSPs in the generation of oscillatory activity. Accordingly, whole-cell patch clamp recordings reveal the presence of phase-locked gamma-frequency IPSCs and EPSCs, respectively. While many of the underlying mechanisms, such as the pivotal role of IPSPs (see below for role of phasic EPSPs) in phasing principal neuron activity, are very similar to the models describe above, pyramidal neurons only fire sporadically, often at less than 5% of the cycles. Thus, with respect to the low involvement of pyramidal neurons this paradigm resembles gamma rhythms generated by pressure ejection of glutamate, clearly demonstrating that individual cells can fire at frequencies well below that of the oscillating network.

Combinations of observations from the above models of synaptically controlled fast inhibition-based oscillations have led to the formulation of a series of hypotheses for the generation of oscillations within the gamma/beta range as controlled by inhibitory neuronal activity. These hypotheses have led to the computer and mathematical modelling of such network behaviours in a remarkably accurate and detailed manner. The basic principles of these models are outlined below and such models, in turn, have fuelled further experimental work via their powerfully predictive nature.

Understanding network oscillations is complicated, in part because of the many nonlinearities present in intrinsic membrane properties, and in the kinetics and interactions of synaptic conductances. Modelling is therefore an important component of the investigation of oscillations in neuronal populations.

We have used two complementary modelling techniques, "detailed" (Traub et al. 1996; Traub et al., 1999), and "reduced" (Ermentrout and Kopell 1998; Karbowski and Kopell, in press). In "detailed" models, one tries to capture some of the complexity of individual neurons, and of the synaptic connectivity, although naturally neither of these can be accomplished in a completely faithful way. Some of the principles involved are these: a) use models of single neurons that contain dendrites, soma, and part of the axon, and use several voltage-gated channel types, with kinetics based (at least partly) on voltage-clamp data. This is necessary to allow the neurons to fire either repetitive action potentials or intrinsic bursts, depending on stimulation conditions, and it allows neurons to integrate synaptic inputs in a reasonable way. It furthermore allows for the possibility of ectopic axonal action potentials, of antidromic spikes, and of gap junction coupling between different sites on the membrane - all of these elements are of possible significance in certain types of oscillations. b) Use enough neurons, and different types of interneurons, to replicate the actual size (at least approximately) of the biological network (i.e. thousands of neurons), and to allow for IPSPs to develop on different parts of pyramidal cell membranes. This allows one to consider the effects of network size and connectivity, and to study the important effects of axonal conduction delays in spatially distributed networks.

The "reduced" models deal with a small number of neurons, with the aim of understanding the essential features necessary for a particular dynamic behaviour. A reduced model depends on what feature is under investigation. For example, in dealing with synchronization of networks of interneurons, a minimal model has two interneurons, each with one compartment. Investigating synchronization in a network of excitatory pyramidal neurons and interneurons requires at least two cells of each type. The models used to understand synchronization in the presence of conduction delays must represent each site. The small models are amenable to analysis, which allows us to tease out from the complex biophysical interactions a deeper explanation of a particular behaviour than is possible from simulations. There are two types of reduced models represented in this work. In the first (White et al., 1998; Chow et al., 1998), there are simplifications in the number and types of neurons, and the anatomy of the neurons, but one still works with the resulting voltage-gated conductance equations. The second kind, used for investigating synchrony over distances, takes the high-dimensional differential equations associated with even a small network and reduces that further to a low dimensional map analysis (Ermentrout & Kopell, 1998). The reduction keeps information about the physiological parameters, so it is possible to use the analysis to make predictions about the effects of parameter changes on behaviour, predictions that can then be tested in the large biophysical models and in experiments.

Using the above techniques, the nature of inhibition-based rhythms and the mechanisms by which these rhythms manifest themselves in neuronal networks has begun to be elucidated. A number of emergent rhythms are possible (and have been observed) in networks where neuronal spike generation is controlled by phasic inhibitory potentials. The following sections deal initially with the mechanisms behind the generation of phasic inhibition and then proceeds to describe how this mechanism can interact with factors such as changes in intrinsic neuronal properties and excitatory network connectivity to produce variations on the fundamental inhibition-based gamma oscillation.

The general concept of an inhibition-based network oscillation centres upon the mutual inhibition of a population of interconnected inhibitory interneurons. The activation of the interneurons can be either tonic (as with application of a metabotropic agonist in the presence of ionotropic glutamate receptor blockers), or phasic (as in the carbachol model) or both (the tetanus model). In the case of the carbachol model the phasic activation of interneurons is generated by the synchronous firing of excitatory neuronal axons in the neocortex and area CA3 of the hippocampus. The degree and extent of this inhibitory neuron to inhibitory neuron connectivity can therefore theoretically govern whether or not an area is capable of generating such an oscillation when excitatory neurons do not participate. In the hippocampus inhibitory connections between GABAergic neurons have been directly demonstrated using recordings of synaptically connected basket cell pairs in the CA1 area (Cobb et al., 1997). Likewise, following the stimulation of afferent fibres, such as the Schaffer collateral pathway, presumably locally generated di-synaptic IPSPs could be elicited in several classes of anatomically identified interneurons (Buhl et al., 1994; 1996). Moveover, these findings are also corroborated by a wealth of anatomical data, showing, for example, the interconnectivy of hippocampal CCK- and parvalbumin-containing basket cells (Nunzi et al., 1985; Katsumaru et al. 1988; Sik et al., 1995). Interestingly, the degree of interneuronal connectivity is strongly dependent on their anatomical or neurochemical phenotype. While axo-axonic cells exclusively target principal neurons, several classes of interneuron are specialised to innervate other interneurons (Buhl et al., 1994; Gulyas et al, 1996).

It is unlikely that these findings are a specialised feature of the hippocampal cortex, but more probably constitute salient principles of neuronal microcircuitry which are also realised in neocortical areas. Thus, in the sensory neocortex, it has been shown that several different types of GABAergic interneurons show a high degree of mutual interconnectivity (Tamas et al., 1998). Intriguingly, basket cells, which are characterised by a preferential perisomatic innervation of their target neurons, were shown to be more strongly interconnected than interneurons belonging to dissimilar classes (Tamas et al., 1998). Therefore, it is apparent that interneurons not only differ in their postsynaptic target preference, with respect to both domain- and cell type-specific innervation, but also regarding the differential degree of their efferent connectivity. It is hence likely that distinct classes of interneuron may have a differential involvement in the generation of interneuron network gamma (ING), depending on the degree of their mutual interconnectivity as well as their domain-specific innervation, e.g. dendrite-targeting interneurons vs. those innervating the perisomatic domain. Finally, certain interneurons may also show a substantial degree of autaptic self-innervation (Cobb et al., 1997; Tamas et al., 1998), thus forming a monosynaptic inhibitory feedback loop which may contribute to pace the activity of individual neurons in the gamma-frequency (i.e. an inhibitory network with a single neuronal element).

The role of intrinsic neuronal properties.

The interneuron population must consist, at least in part, of neurons with intrinsic firing frequencies faster than the population rhythm. Firing frequencies higher than the gamma range (more than 80 - 90 Hz) are common in directly depolarised inhibitory interneurons in the CNS (eg Buhl et al, 1994; 1996; Whittington et al., 1997). If a population of such neurons is excited, then the firing frequency of the population response is governed by the timecourse of the mutual inhibition present from one neuron within the population to its synaptically connected neighbours (Whittington et al., 1995; Traub et al., 1996b; Wang & Buzsáki, 1996; White et al., 1998; Chow et al., 1998). Figure 2 illustrates this general principle. For a single interneuron, depolarisation results in a train of action potentials whose frequency is governed by the degree of depolarisation and the timecourse of the spike afterhyperpolarisation (AHP) that constitutes the relative refractory period of the cell. If the cell is depolarised to a level above sodium spike threshold then an action potential is generated. Following this action potential is an intrinsic AHP generated by the transient depolarisation produced by the action potential. No further spike is generated until this AHP fades to a potential level above spike threshold (fig 2A).

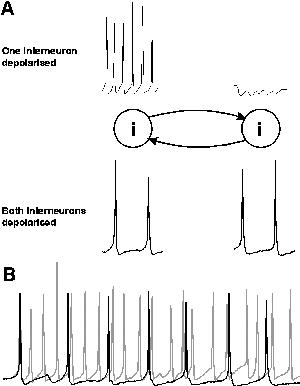Figure 2

If a population of interconnected interneurons are depolarised then each action potential will generate an inhibitory postsynaptic potential (IPSP) in each connected target interneuron. If enough interneurons fire action potentials at approximately the same time then convergent inhibitory inputs generate a temporally summated IPSP of sufficient magnitude to prevent further action potential generation until the IPSP fades. The time from the first to subsequent action potentials is therefore influenced not only by the intrinsic AHP but also the synaptic inhibitory potential. The time between action potentials in this situation is governed by the time course of the AHP and that of the IPSP (see White et al., 1998. The time courses of AHPs and IPSPs were also implicated in Wang & Rinzel (1993) in bursting thalamic reticular cell models). If the IPSP timecourse is comparable to that of the AHP then this situation will not affect the spike - spike periodicity (frequency). However, the timecourse for IPSPs from one interneuron to another is approximately four-fold slower than the AHP. Thus when networks are activated the spike frequency is controlled by the timecourse of the mutual IPSPs (fig 2B, see below).

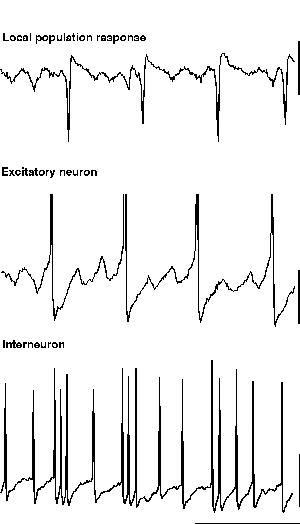
The experimental model of pure interneuron network gamma oscillations (ING) is almost certainly an artificial situation (but see possible exceptions above). In the majority of mapped networks in the CNS, activity in excitatory neurons exerts an influence on inhibitory neurons and vice versa. As mentioned in the models section above, to see the inhibitory network behaviour in isolation drugs must be applied to an in vitro preparation to pharmacologically separate excitatory synaptic activity from inhibitory synaptic activity. This can be done relatively simply in an experimental environment by the application of specific antagonists of the major fast excitatory components of synaptic transmission (Whittington et al., 1995; Whittington et al., 1996; Traub et al., 1996b). In the presence of drugs which block the NMDA and AMPA subtype of glutamate receptor-mediated excitation, ING can be studied by monitoring the activity of individual interneurons or by observing the influence of populations of oscillating interneurons on target excitatory neurons. The model most suited to this end is that using pressure ejection of glutamate or specific mGluR agonists onto the hippocampal CA1 subfield (fig. 3) or superficial layers of neocortex (model i) above).

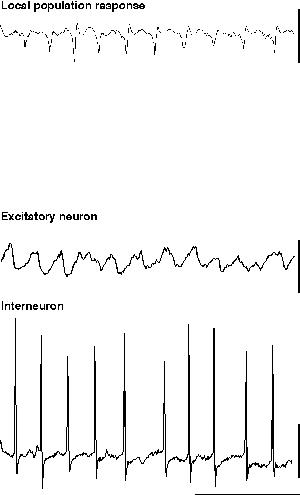Figure 3

Results from studies using this model have characterised the dependence of the basic frequency of network oscillation on two major parameters; 1) the magnitude and kinetics of the GABA_A receptor-mediated inhibitory synaptic potentials between interneurons, and 2) the magnitude of tonic driving force (Whittington et al., 1995; Whittington et al., 1996; Traub et al., 1996b; Wang & Buzsáki, 1996; Chow et al., 1998). The case for these statements is set out below.

1) The magnitude of the synaptic inhibition between interneurons governs the frequency of ING. This is the case for both absolute magnitude changes in the postsynaptic response and the kinetics of the response itself. A broad range of endogenous and exogenous agents can modify the GABA_A receptor mediated IPSP and many of these have been shown to alter the frequency of gamma oscillations in experimental models (for review see Whittington et al., 1999). These agents include anaesthetics (Halothane (MacIver et al., 1991), sedatives (diazepam (Segal & Barker, 1984), hormones (Insulin (Wan et al., 1997), Sex steroids (Teschemacher et al., 1995)) and other neuromodulators (eg. Siarey et al., 1995).

Experimentally, the amplitude of the IPSP can be altered with little effect on macroscopic current kinetics by benzodiazepines positively and bicuculline negatively. Application of diazepam to an oscillating brain region increases the amplitude of the trains of IPSPs which generate ING and produces a concentration-dependent decrease in frequency (Traub et al., 1996b). In contrast, reduction of IPSP amplitude via the GABA_A receptor antagonist bicuculline, or reduction of GABA release with morphine, increases the frequency of ING (Traub et al., 1996b; Whittington et al., 1998). Inhalational anaesthetics, propofol and anaesthetic barbiturates can all increase the duration of IPSPs with little effect on total charge transfer during the postsynaptic event. These agents all cause a marked decrease in ING frequency, so much so that high concentrations reduce frequency to a point where ING is no longer supported. In contrast morphine decreases GABA release, reduces the amplitude of the IPSP and causes an increase in frequency (Whittington et al., 1996; 1998, fig 4). These observations demonstrate the nature of ING and highlight the role played by the IPSP in generating and controlling oscillation frequency. From this a prediction can be made that any pharmacological agent or neuromodulator substance that affects the kinetics of the GABA_A response, the amount of GABA released at inhibitory terminals, or the excitability of interneurons themselves, will affect the rhythmicity and frequency of gamma oscillations generated by inhibitory neuronal networks.

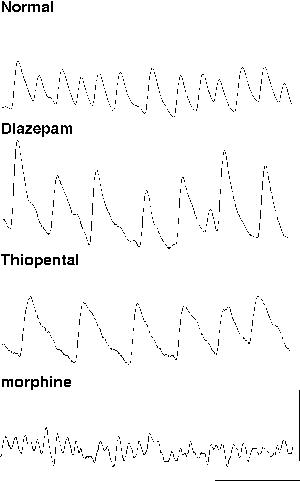Figure 4

2). The tonic driving force causing the excitation of the interneuron network has to be of sufficient magnitude: it must be large enough to cause individual interneurons (were they to be synaptically uncoupled from the network) to fire faster that the frequency produced by the network as a whole (i.e. the gamma band). As driving force decreases from optimal a decrease in the frequency of the population oscillation can be seen until the population oscillation is no longer manifest. This usually occurs at frequencies around 15 Hz (Traub et al., 1996b). As driving force increases, oscillation frequency can also increase (up to c. 80 Hz) but, in the case of mGluR activation, the dependence of frequency on drive is non-linear, and experimentally ‘over-excited’ networks can demonstrate a decrease in oscillation frequency. In other words, using mGluR activation to drive a population of interconnected interneurons produces an oscillation whose frequency can vary within the gamma and beta EEG bands but not outside these bands.

Simulations and theory have clarified the mechanisms behind these observations by showing that the limited range is related to the ability of the network to create a synchronous rhythm. Wang and Buzsaki (1996) gave simulations demonstrating that, in the presence of heterogeneity, the coherence breaks down, but breaks down least when the parameters are such that the frequency is in the gamma range. Analysis by Gerstner et al (1996) and van Vreeswijk et al (1994) showed that homogeneous networks can synchronize at a wide range of frequencies (both higher and lower than the gamma range); Chow et al. (1998) showed that the network frequency in such a homogeneous network can be governed by other time scales than inhibition. But if the cells are driven to be faster or slower than that range, and there is heterogeneity in the network, White et al. (1998) showed that the coherence will break down in predictable ways. Furthermore the analysis in Chow et al. (1998) said that, in the range in which coherence is greatest, the network period should be linearly proportional to the decay time of the inhibition, a result that matches the data in Whittington et al. (1995). Related work on the effects of IPSP timecourse on coherence (but not frequency) of bursting thalamic reticular cells has been done by Wang and Rinzel (1993) and Terman et al. (1998). According to the theory, other parameters, such as the amplitude of the synaptic inhibition (see above), should also affect the frequency, but not as strongly. Thus, for reasons of intrinsic properties of the cells (response to mGluR or mAchR activation) and constraints imposed by coherence, using metabotropic activation to drive a population of interconnected interneurons produces an oscillation whose frequency can vary only between roughly 15-80 Hz.

ING alone is unlikely to represent a specific mode of information processing in the CNS. However, the information that experiments and models has revealed about inhibitory networks in isolation has been successfully applied to models in which network connectivity is present in its entirety. For ING to be important physiologically it must influence (even tightly control) the firing patterns of excitatory projection neurons. This occurs in situations where metabotropic receptor activation (mGluR, Whittington et al., 1997; mAchR, see below) not only generates the ING but also recruits pyramidal cells. In such a situation, in an intact local network, the activity of excitatory neurons will, in turn, modify the behaviour of the interneuron network via feed back excitation of interneurons. Thus an oscillation is produced involving the interplay between excitatory pyramidal cells and interneurons; pyramidal interneuron network gamma (PING). From a theoretical perspective PING can be modelled using purely phasic excitatory drive to ‘pace’ interneuron networks. Using this approach in modelling has led to considerable progress in the understanding of mechanisms controlling oscillations in networks containing excitatory and inhibitory neurons (mixed networks). In the experimental situation, varying degrees of phasic- compared with tonic drive to inhibitory interneurons can be seen using the models discussed above. Though the degree of tonic drive influences the ability of an interneuron network to generate ING (see previous section), the superimposition of a phasic drive can be an essential component controlling oscillatory behaviour in mixed networks.

ING alone produces rhythmic trains of IPSPs in pyramidal cells which would be expected to influence the timing of action potential responses to afferent excitatory input. However ING does not generate an excitatory projection neuron output de novo. If excitatory neurons are concurrently depolarised along with the inhibitory network then the IPSP trains can generate precisely temporally controlled action potentials in these neurons. However, many excitatory neurons in the CNS have calcium-activated potassium conductances which markedly attenuate long periods of spike generation. The consequence of this is that, without metabotropic activation, excitatory neurons cannot participate in inhibition-based gamma and beta oscillations for longer than a few periods. Metabotropic glutamate (and acetylcholine) activation alters this situation by reducing the magnitude of a number of potassium conductances that take part in the post-spike AHP (see fig. 10. Charpak et al., 1990; Storm, 1989). If these longer-duration hyperpolarising voltage transients are attenuated to such an extent that the IPSP is the longest duration significant post-spike event in excitatory as well as inhibitory neurons, and if the excitatory neurons are depolarised, then these excitatory neurons will fire repeated action potentials at gamma frequencies along with, and synchronously with, the local interneuron network (fig. 5).

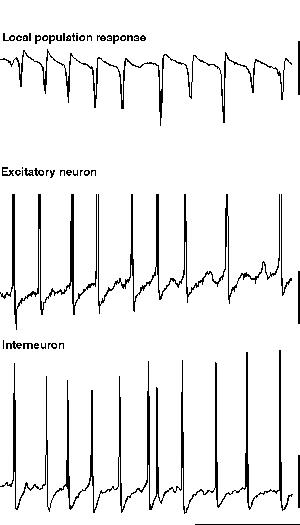Figure 5

Large-scale involvement of pyramidal cells in an inhibition-based gamma oscillation occurs during the gamma oscillation induced by tetanic stimulation (Whittington et al., 1997a; Traub et al., 1999). In this case, with long intervals between tetani (< 1 per 3 minutes), excitatory neurons participate in over 80% of periods of the underlying gamma oscillation. As the repetition interval of tetani decreases to more closely resemble that of sharp waves in vivo (> 1 per minute) the excitatory drive to the excitatory neurons attenuates to produce an oscillation more reminiscent of ING (i.e. with low drive to excitatory cells with respect to inhibitory neuronal drive. Doheny et al., unpublished observations). With the large-scale involvement of excitatory neurons large excitatory postsynaptic potentials (EPSPs) are seen in interneurons during the gamma oscillation (Whittington et al., 1997b; Traub et al., 1999). These EPSPs are mediated predominantly by the AMPA subtype of glutamate receptors (Whittington et al., 1998; Traub et al., 1999). The kinetics of these EPSPs are very fast and are ideal for the fine control of interneuron firing in the temporal domain (Whittington et al., 1998; McBain et al., 1999). The EPSPs serve a number of functions within the dynamics of a local gamma oscillation: They cause a relative stability of the oscillation (in terms of frequency and coherence) with respect to changes in interneuron IPSP amplitude and kinetics. EPSPs in interneurons can also lead to spike doublets that allow spatially separated - but interconnected - regions to oscillate synchronously (see below). EPSPs in excitatory neurons can act to project an oscillation in one region to other connected brain regions (Whittington et al., 1997b; Faulkner et al., 1998; Colling et al., 1998).

The stability afforded by excitatory pyramidal cell involvement in network gamma can be demonstrated by comparing the effect of agents that change IPSP parameters on the frequency of oscillation in the presence or absence of active excitatory neuronal involvement. For example maximal reduction in frequency of oscillation afforded by diazepam was 50% for isolated interneuron network gamma, but only 20% for oscillations where excitatory cells also participate (see Whittington et al., 1996 and Faulkner et al., 1998). Similarly, thiopental, at a concentration of 50 µM, caused a 70% reduction in ING frequency but only a 40% reduction in frequency when excitatory neurons were involved.

The above observation leads us to a working definition of the ING and PING rhythms, with some networks that include excitatory pyramidal cells behaving like ones with only interneurons (as above). The central difference is which class of cells (on the whole) acts to pace the network. In an ING rhythm, the interneurons recover from inhibition and fire without excitation from other cells; as mentioned in the section on ING, these cells must then have sufficient drive to be able to fire even in the presence of inhibition, so their natural firing rate would be larger than the gamma frequency (as demonstrated above). The excitatory pyramidal cells are then basically gated by the rhythm created by the interneurons, and fire in the periodic intervals when the inhibition is low. If the drive to the excitatory neurons is relatively high (but not so high that they fire before the interneurons on a given cycle), then these excitatory neurons can fire in most cycles and still have an inhibition-driven rhythm (ING). (See the next section for sparse involvement of the excitatory neurons.)

What then constitutes an idealised PING rhythm is one in which the excitability of the excitatory neurons is such that the latter recover from inhibition before the inhibitory cells do; the resultant firing of (at least some) of the excitatory neurons then causes the interneurons to fire. Note that, in a PING rhythm, agents that change the size and time course of inhibition have an effect that depends on the excitability of the excitatory neurons, while for ING rhythms their effect depends on excitability of the interneurons alone. This accounts for why there is a difference between the effects of GABAergic drugs in the full slice network, and when the ionotropic synaptic excitation is blocked. Also note that changing the relative excitability of the interneuron and excitatory neuron populations can change the rhythm from an ING to a PING rhythm or vice versa.

The active involvement of excitatory neurons in the rhythm also makes the network much less vulnerable to loss of coherence when there is heterogeneity in driving forces (Traub et al 1996b; Wang & Buzsáki, 1996; White et al., 1998). In simulations of networks involving both excitatory pyramidal cells and interneurons, assuming that the drive to the interneurons is narrowly dispersed (e.g., under 10%), the drive to the excitatory neurons can vary as much as two-fold and still get coherence with approximate synchrony (Traub et al., 1997).This is due to two main factors: Firstly, the interneurons fire, at least in part, because of tonic excitation, and not just from phasic EPSPs coming from the excitatory neurons; second, the excitatory neuron -> interneuron connections act to average the synaptic excitation produced by the excitatory neuronal firing - provided that the excitatory neuron->interneuron connections are not too powerful, and that there is not too much recurrent excitation between participating excitatory neurons. That is to say, there are different dynamical mechanism for synchronization than in rhythms with only interneurons. In the latter, synchronization comes from changes in timing of the interneurons on successive cycles due to different timing of inhibitory inputs; this is fragile and easily vulnerable to suppression, in which the cells with lower excitability fall out of the population (White et al., 1998). When there are pyramidal cells in the network, convergence and divergence of the connections between the excitatory and inhibitory neurons provide an alternative and more robust mechanism for synchronization: the interneurons receive input from the population of the pyramidal cells, and hence act to average the excitation in the network. In a PING-type rhythm, in which the firing of the interneurons depends on the timing of the excitation, such averaging produces coherence of the interneurons, which then gates the timing of the pyramidal cells. With a large dispersion in drives to the excitatory pyramidal cells, the latter are not exactly synchronous, but fire in a window determined by the inhibitory rhythm.

In addition to the effects of EPSPs in interneurons on the stability of locally generated gamma rhythms, these EPSPs also allow spatially separated sites (with intersite conduction delays of several ms) to oscillate at gamma frequencies with approximately 1 ms mean phase differences. This occurs experimentally using the tetanus when there are 2 stimulating electrodes in the CA1 region of hippocampal slices, with spacing between the stimulated sites of about 1 mm up to at least 4.5 mm (Traub et al. 1996b; Whittington et al. 1997). How does this remarkable effect occur? Consider an interneuron at one site: it will be synaptically excited, almost immediately, by the synchronous firing of nearby excitatory neurons; and, it will be excited, after an axon conduction delay, by the synchronous firing of distant excitatory neurons at the second oscillating site. If the two sites are approximately in phase, and if the excitatory neuron/interneuron connections are strong enough, then the later EPSP should be able to generate a second interneuron spike, a few milliseconds after the first interneuron spike that occurs nearly in phase with nearby excitatory neurons. Such a spike pair is called a doublet. The existence of doublets was predicted on theoretical grounds, and shown to occur experimentally during 2-site oscillations, but very rarely during 1-site oscillations (Traub et al. 1996b, Whittington et al. 1997b; Traub et al. 1999). Experimental manipulations, such as AMPA receptor blockade, that interfere with doublets also interfere (as expected) with 2-site synchrony (Whittington et al. 1997a; Traub et al. 1999).

How interneuron doublets can produce stable synchrony of two sites has been analysed carefully by Ermentrout and Kopell (1998), using a reduced model. In part, the interspike interval of the doublet acts as a feedback signal that encodes the phase separation of the two sites, and generates a correcting signal - relatively advancing or delaying the time of the next excitatory neuronal spikes at either site. Interestingly, this encoding is not sufficient for the mechanism to work. The relative refractoriness of the interneuron membrane also plays a role; that is, an EPSP occurring soon after an interneuronal spike leads to a second interneuronal spike only after some delay, and this delay tends to shorten the more delayed the EPSP is (other things being equal). The importance of this effect could not have been predicted without mathematics.

Doublets act to synchronize 2 sites in part because the doublet timing is determined by when the pyramidal cells fire; this feature of the system is favoured by the fast kinetics of AMPA receptor-mediated EPSPs in interneurons (Miles, 1990; Whittington et al. 1998; McBain et al. 1999). When the precision of synaptic interactions is disrupted, then the precision of 2-site synchrony also suffers. One experimental means to accomplish such disruption (which can also be modelled) is with bath application of morphine, a drug that reduces GABA release at terminals on both interneurons and on excitatory pyramidal cells (Madison & Nicoll, 1988). In this case, the synaptic output of the inhibitory network is less able to entrain the firing of excitatory neurons. Probably more significant, however, is that - without the normal degree of mutual inhibition between interneurons, but with AMPA receptor-mediated inputs from pyramidal cells interneurons tend to fire in bursts (instead of singlets and doublets) in the presence of morphine. As predicted in this situation, morphine induces clear disruption of 2-site oscillation synchrony, although local gamma oscillations persist (perhaps at somewhat increased frequency, Whittington et al. 1998). A second experimental means of disrupting the precision of excitatory pyramidal cell/interneuron synaptic interactions is by prolonging the time course of AMPA receptor-mediated EPSPs in interneurons. The latter can be accomplished by transgenic techniques involving the expression of the GluRB glutamate receptor subunit in interneurons (Fuchs et al, unpublished data). Again, interneurons are induced to fire in triplets, as well as singlets and doublets, during 2-site gamma oscillations; and again, as predicted, 2-site synchrony is severely disturbed.

In vivo recordings of gamma oscillations in hippocampus and neocortex have a degree of excitatory neuron involvement which generally lies somewhere between the above two extremes. Owing to the high degree of connectivity between excitatory and inhibitory neurons in these areas, and the fact that the majority of afferent inputs to these areas activate both neuronal types during an oscillation (Burchell et al., 1988), it is unlikely that excitatory neurons play no part (as in ING). Involvement of large proportions of excitatory neurons in neocortical gamma oscillations is also highly unlikely given the high degree of anatomical localisation of function of these neurons in primary sensory areas. However, excitatory neurons do contribute to neocortical gamma in a highly specific fashion (eg in the visual system, Schmidt et al., 1997), and the demonstration of gamma oscillations in local field potential recordings (Singer & Gray, 1995) strongly suggests a high degree of pyramidal cell involvement, at least in specific localised regions. Given the divergent nature of excitatory synaptic connections between excitatory neurons and interneurons, large-scale involvement of excitatory neurons is unlikely to be necessary to account for the differences in ING and PING highlighted above.

Two models have been developed that demonstrate gamma oscillations where excitatory neuronal involvement is only partial on a period-by-period basis: Pressure ejection of glutamate or specific mGluR agonists in the absence of other pharmacological intervention generates field potential gamma oscillations with excitatory neurons firing on approximately 20% of periods (Burchell et al., 1998). As noted above, bath application of carbachol (a muscarinic cholinergic agonist) also generates field potential gamma oscillations, in this case with an even lower degree of excitatory neuronal involvement (approximately 5% of periods of gamma oscillation (Buhl et al., 1998; Fisahn et al., 1998). These models represent significantly different methods of generating a network gamma oscillation using interneuron networks and will be considered separately here.

When glutamate is pressure ejected onto a region of hippocampus in the absence of blockade of ionotropic glutamate receptors, field potential electrodes can record a population oscillation at gamma frequencies (c. 40 Hz). Intracellular recordings from interneurons reveal the characteristic train of action potentials generated from a tonic depolarisation superimposed on which are trains of IPSPs from the interneuron network (fig. 5). Recordings from individual excitatory neurons also shows the tonic depolarisation and the train of IPSPs at gamma frequencies (Burchell et al., 1998). However, unlike the rhythm produced by tetanus (fig. 5), here excitatory neurons fire, on average, on every fifth period of underlying gamma (ie. at approximately 5 Hz). The periods upon which an individual excitatory neuron will fire an action potential appear to be randomly determined under these conditions (but see below). Thus a field electrode records a similar, though smaller in amplitude, population oscillation to that seen with much larger excitatory neuronal involvement (compare fig 5 & 6). The probability of each individual excitatory neuron producing an output at gamma frequencies is very low, and removing excitatory influences on the inhibitory network (via ionotropic glutamate receptor blockade) does not ablate the inhibitory network gamma oscillation. Therefore it appears that, under these conditions, the train of inhibitory potentials invading all excitatory neurons within the oscillating area simply acts to provide a temporal framework within which afferent excitatory input can be gated (Burchell et al., 1998).

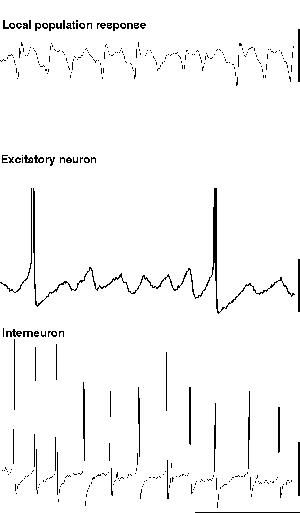Figure 6

When persistent oscillations are generated in hippocampus or neocortex via the tonic activation of muscarinic cholinergic receptors or group I mGluRs, then the role of excitatory neurons is somewhat different from the tetanic and ING models described above (Buhl et al., 1998; Fisahn et al., 1998). It appears, that under these conditions the degree of tonic excitation of interneurons is not sufficient to maintain ING in the presence of AMPA/kainate antagonists. Thus, phasic excitation, originating in recurrent excitatory feedback loops, assumes a greater role in the generation of gamma-frequency network oscillations. Nevertheless, recordings from interneurons and pyramidal cells do demonstrate the same basic features of the inhibition-based rhythm seen in other models (compare fig 6 & fig 7). Although pyramidal cells fire more sporadically, concomitantly recorded interneurons discharge vigorously, often at or near gamma frequency, thereby generating rhythmic IPSPs in neighbouring pyramidal neurons. Moreover, in pyramidal neurons the probability of action potential generation increases in parallel with the decay of IPSPs, which is commensurate with their role in phasing population activity. Accordingly, barbiturates, by virtue of increasing IPSP duration (see above), decrease the frequency of the gamma-band network activity.

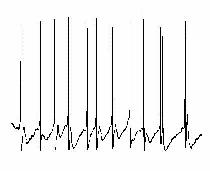Figure 7

Beta oscillations, from an EEG perspective, represent rhythms with a frequency in the band below gamma (i.e. 30 Hz down to alpha frequencies). However, whether there is a clear delineation from gamma to beta using this nomenclature is debatable, particularly as a number of researchers refer to gamma as beta (eg see Leung, 1996). From an oscillation dynamics perspective this difficulty in separating gamma from beta oscillations is also apparent. However, experiments have revealed that within the classical beta bands (12 - 30 Hz) at least two dynamically different forms of inhibition-based oscillation can be generated both in vitro and clinically (Traub et al., 1999; Faulkner et al., 1999; Baldeweg & Gruzelier, personal communication). These forms of beta have different stabilities and different synchronising properties when compared with gamma oscillations, so that they may represent different mechanisms of CNS function at the holistic level (see von Stein et al., 1999; Kopell et al., 2000).

The simplest form of beta oscillation can be thought of as a slow gamma oscillation in any of the guises described above (fig 8). To generate a beta oscillation in this manner the factor controlling periodicity (i.e. the size and shape of the interneuron network IPSP) can be altered. This can be done experimentally in two ways: Firstly, the decay constant for the network IPSP can be prolonged artificially by application of GABAergic drugs such as barbiturates, inhalational anaesthetics or propofol (Whittington et al., 1996; Fisahn et al., 1998; Whittington et al., 1999). In this case the periodicity of the population oscillation can be reduced by over a factor of two, transforming a gamma (c. 40 Hz) oscillation into a beta (c. 20 Hz) oscillation. Such agents are commonly used in the clinical environment to induce and/or maintain anaesthesia. One of the most common EEG correlates of induction of anaesthesia is the presence of a ‘beta buzz’ which may represent the transformation of on-going gamma activity to this form of beta oscillation. Secondly, an increase in the size of the IPSP relative to the degree of driving force behind the oscillation can reduce fundamental frequency down to within the beta range. This can occur experimentally either by application of benzodiazepines, to potentiate IPSP amplitudes (Whittington et al., 1996), or by a reduction in the tonic driving force itself (Traub et al., 1996). In the case of potentiated IPSPs beta oscillations are only seen in isolated interneuron networks (ING). With strong recruitment of excitatory neurons the frequency of oscillation is more robust (see above) and remains within the gamma band (Faulkner et al., 1998). Computer simulations of oscillation-based learning in networks have shown that potentiation of IPSPs can also generate beta in response to ‘recognition’ of specific patterns of network activation (Bibbig, 1999. see below). In the case of reduced tonic drive the decrease in frequency is also accompanied by a decrease in the strength of the inhibition-based oscillation. This is possibly a consequence of the variability in depolarisation from neuron to neuron (so called heterogeneity, see above) becoming a more appreciable fraction of absolute depolarisation. For ING to remain coherent, excitation of interneurons must not be too heterogeneous (White et al., 1998).

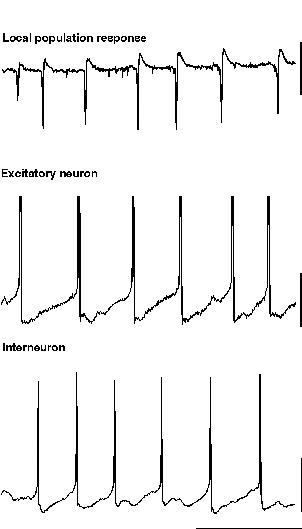Figure 8

The second form of beta oscillation which can be seen to arise from inhibition-based rhythms is fundamentally different, in that the interneurons continue to oscillate at gamma frequencies, while excitatory neurons oscillate at beta frequencies coherently with each other (Whittington et al., 1997; Traub et al., 1999). As with the excitatory neuronal response seen during population gamma (above), excitatory neurons are seen to fire only on a proportion of periods of the underlying interneuron rhythm (fig. 9). The critical difference, both from the appearance of the field potential oscillation and a mechanistic point of view, is that many excitatory neurons in the oscillating population fire action potentials on the same period of underlying gamma. This situation leads to field potential waves occurring at beta frequencies. Thus the average activity of excitatory neurons does not generate a gamma frequency oscillation. Instead the excitatory neuronal activity sums to generate a field oscillation at some subharmonic frequency of the underlying gamma. The absolute value of this frequency depends on the number of beats of interneuron firing missed between firing of the larger proportion of excitatory neurons.

Figure 9

The reasons for this more complex behaviour of excitatory neurons in beta than in gamma activity appear to be three-fold. Firstly, with tetanically-induced rhythms ‘missed beat’ beta is more commonly associated with maintained or enhanced tonic depolarisation of neurons in the oscillating population. This happens because, when tetanically induced depolarisation is brief, then gamma alone occurs; while if the depolarisation lasts sufficiently long, gamma followed by beta activity is seen (i.e. a beta oscillation is seen as a consequence of continued excitatory drive following periods of synchronous gamma oscillation). Secondly the intrinsic AHPs generated after action potentials in excitatory neurons are much greater during missed-beat beta than during population gamma. The combination of these two factors produces a strong interneuron network gamma oscillation which provides the temporal framework for controlling excitatory neuronal firing. The excitatory neurons themselves remain depolarised and should follow the interneuron network rhythm. However, thirdly, the AHPs seen during this form of beta are so large that these neurons remain in relative refractoriness for a time greater than one period of the IPSP generated subthreshold rhythm. Thus, the lack of firing on each period of gamma is a consequence of the constraints upon the upper limit of firing frequency of excitatory neurons and is not a consequence of borderline tonic excitation. This difference alone does not explain the local synchronisation of excitatory neurons at beta frequencies: To generate the degree of synchronisation of excitatory neuronal output seen, the firing of a single excitatory neuron must positively influence the probability of action potential generation in others.

The ability of one excitatory neuron to influence another is afforded by activation of recurrent excitatory connections (Whittington et al., 1997; Traub et al., 1999). Anatomically the degree of connectivity between excitatory neurons (recurrent excitation) is both sparse, compared with excitatory connections to inhibitory neurons, and highly variable between brain regions. For example, estimates of recurrent connectivity in hippocampal area CA1 are low (1 in 130 cell pairs, Thomson & Radpour, 1991), but in hippocampal area CA3 and the neocortex connectivity appears to be higher (1 in 60 for CA3, Miles & Wong, 1986; 1 in 30 for neocortex, Thomson et al., 1988). These connections also appear to show a degree of plasticity such that periods of synchronous oscillatory activity produce a potentiation of the excitatory synaptic potentials (Whittington et al., 1997; Faulkner et al., 1999).

Experiments using tetanic stimulation to generate PING in hippocampal area CA1 demonstrate measurable excitatory synaptic potentials, both from excitatory neuron recordings and field recordings. These potentials occur at beta frequencies during the field potential beta oscillation. In models where intrinsic currents (mainly AHPs, above) are modified to produce missed beats the connectivity between excitatory neurons has been shown to be critical for coherent beta oscillations (Kopell et al., 2000). However, the reasons for this are not straightforward. A number of reduced-model equations have shown that direct connections between excitatory cells can have the effect of preventing synchronization (van Vreeswijk et al, 1994; Gerstner et al., 1996). Crook et al (1998) have shown that with the appropriate intrinsic currents in excitatory pyramidal cells, the excitatory connections can be synchronizing. It can be seen from the reduced biophysical models that the transformation from gamma to missed-beat beta also relies on having appropriate ranges of drives for the excitatory and inhibitory cells. For example, if the drive to the interneurons is lowered, even if the excitatory cells are slowed and there are excitatory to excitatory connections, the network will display a slow gamma rhythm rather than beat-skipping beta.

.

The types of inhibition-based oscillation described above and elicited via glutamatergic receptor activation are not mutually exclusive. Small changes in the critical parameters controlling the generation and maintenance of these oscillations can transform one type of oscillation into another. The relationship between ING and PING is governed principally via the degree of excitatory neuronal involvement in spike generation in interneurons. On a sliding scale excitatory neurons are seen to be committed to each period of the network oscillation either not at all (ING), partially or almost completely (PING). As each resulting population oscillation is at gamma frequencies, and has the same underlying mechanism (activation of a network of mutually inhibitory interneurons), this transition is afforded principally by the relative degree of activation of excitatory neurons within the network (and the consequent phasic drive to interneurons) and by the possibility that - in PING- interneuron doublets can occur. Doublets can allow long-range synchrony, as described above, and also slow the oscillation frequency somewhat, by generating longer-lasting IPSPs than interneuron singlets.

A number of factors may influence how many excitatory neurons participate in gamma activity. The relative depolarising drives to excitatory neurons and inhibitory neurons principally govern the possible degree of excitatory neuronal involvement. Predominantly metabotropic glutamate receptor-mediated activation of a region (as in ING and models with sparse excitatory involvement) appears to drive interneurons more effectively than excitatory neurons. Both neuronal types possess mGluRs but certain types of interneuron appear to be more sensitive to agonists than other cells (eg. McBain et al., 1994). In excitatory neurons depolarisations have been reported for mGluR activation via two mechanisms: 1) A depolarisation mediated by increases in input resistance secondary to a blockade in potassium channel conductances (Davies et al., 1995). 2) An mGluR receptor-mediated excitatory postsynaptic potential associated with a decrease in input resistance secondary to activation of a calcium-activated non-selective cation current (Congar et al., 1997). Excitatory neuronal depolarisation in the tetanus model is also sensitive to blockade by NMDA receptor antagonists (Whittington et al., 1997) and mutual positive interaction between these two glutamate receptor families (mGluR and NMDA) has been reported (Alagarsamy et al., 1999). The additional NMDA component may explain the increase in activation of excitatory neurons in this form of gamma oscillation. Habituation of post-tetanic responses transforms PING oscillations into a predominantly subthreshold ING (fig. 10) and blockade of NMDA receptors with ketamine also dramatically reduces excitatory neuronal drive (Faulkner et al., 1999; Doheny & Whittington unpublished observations). In addition, other researchers have demonstrated a potent depolarising GABA component underlying post-tetanic responses (Bracci et al., 1999). These researchers suggest that the final pathway in depolarising excitatory neurons is this GABA depolarisation, with the glutamatergic effects serving only to enhance GABA release by driving interneurons. However, little, if any, synaptic component to the oscillations following tetanus was seen in the experiments of Bracci et al. while most of our observations on tetanic gamma oscillations (including drug effects and long-range synchrony) can only be explained if the oscillations are gated by synaptic conductances.

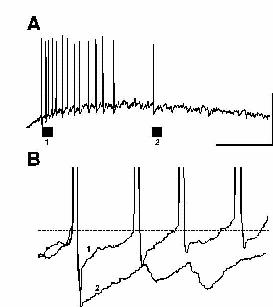Figure 10

Another factor controlling the involvement of excitatory neurons is the magnitude of the post-spike AHP (as described in detail above). In steady-state models generating population gamma a large AHP may contribute to the failure of excitatory neurons to fire on every period of an underlying inhibition-based gamma oscillation (see above). In the tetanus model of PING AHPs are initially suppressed but recover over c. 0.5s (Whittington et al., 1997b, Traub et al., 1999). As this recovery takes place a clear decrease in the recruitment of excitatory neurons is seen (fig. 10).

Transition from gamma to beta oscillation is more complex and is dependent on both relative changes in the intrinsic properties of excitatory neurons (particularly the AHP) and the activation of recurrent excitatory synaptic pathways (Whittington et al., 1997b; Traub et al., 1999; Kopell et al., 2000). Beta is seen experimentally where there is large-scale recruitment of excitatory neurons. Thus beta can occur in the tetanic model of PING and during oscillations induced by potassium transients (Towers, LeBeau & Buhl, Unpublished observations; Patrylo et al., 1994). From our observations the critical feature necessary for transforming gamma to beta population oscillations is the coherence of excitatory neuron firing with respect to each period of the underlying gamma. In the population gamma models above, tonic excitatory neuronal drive and possibly AHP amplitudes conspire to prevent excitatory neurons firing on each gamma period. However, the arrangement of excitatory neuron spikes with respect to the underlying gamma appears to be stochastic - resulting in a net gamma oscillation. If excitatory connections between excitatory neurons are enhanced then this communication serves to increase the probability of each excitatory neuron in a population firing on the same period of underlying gamma (Kopell et al., 2000; Traub et al., 1999).

Other models of gamma to beta transitions involve different parameter changes to those above (Bibbig, 1999). In this case the AHP is not simulated explicitly, and the frequency transition is afforded by potentiation, in a Hebbian fashion, of both a) inhibitory synaptic connections onto excitatory neurons, and b) excitatory connections onto inhibitory neurons. Of these potentiation of IPSPs is the most important for the production of beta per se. This form of beta activity has been shown to facilitate pattern separation during ‘learning’ in arrays of simple model neurons; for pattern separation, potentiation of excitatory neuron - interneuronal connections is predicted to be critical. Experimentally, potentiation of these inhibitory synaptic connections has been seen for rhythmic trains of stimuli between c.10 - 100 Hz (i.e. including gamma frequencies, Jensen et al., 1999).

In general, the frequency of the oscillations covered here is dependent on the duration of the relative refractory period of the neurons involved (but see Traub et al. (1999) for a discussion of oscillations controlled by electrical neuronal connections). There are a number of contributors to this, such as intrinsic AHPs and synaptic inhibitory potentials. The longest of these contributors can ultimately set the fundamental frequency of the respective neurons (see above). The intrinsic neuronal properties which act as contributors are different between excitatory and inhibitory neurons. However, the metabotropic stimuli used to generate inhibition-based oscillations change these parameters, in such a way as to make the firing patterns of excitatory neurons more closely resemble the patterns of interneurons. Furthermore, the generation of inhibitory network activity introduces a common controlling element - the network IPSP.

Oscillations generated by glutamatergic activation and those generated by cholinergic activation may well be mutually excusive. There is pharmacological evidence for co-desensitisation of metabotropic glutamate and acetylcholine receptors (Guerineau et al., 1997). This suggests that a network capable of generating oscillations via either mechanism will do so on a competitive basis. If the major source of drive is cholinergic, as presumed to occur during theta activity, then the continuous, steady state oscillations described by Fishan et al. (1998) will be expressed at the expense of the more transient glutamate-induced gamma oscillations. An in vivo correlate of this may be the habituation of sharp waves. Sharp waves have a gamma tail reminiscent of the post-tetanic response in in vitro models (see above). They are associated with awake immobility, grooming, feeding and slow wave sleep, but are not seen during exploratory activity (Buzsáki, 1986). The occurrence of gamma tails in vivo stands in contrast to oscillations presumed to be generated cholinergically, in as much as sensory stimulation suppresses the occurrence of sharp waves (and hence the gamma tails) in a motionless rat. This occurs whether or not an overt behavioural response or theta activity is observed.

Alagarsamy, S. Marino, M.J., Rouse, S.T., Gereau, R. W., Heinemann, S. F. & Conn, P. J. 1999. Activation of NMDA receptors reverses desensitization of mGluR5 in native and recombinant systems. Nat. Neurosci. 2: 234-40

Antkowiak, B. & Hentsche, H. 1997. Cellular mechanisms of gamma rhythms in rat neocortical brain slices probed with the volatile anaesthetic isoflurane. Neurosci. Lett. 231: 87-90.

Barth, D. S. & MacDonald, K. D. 1996. Thalamic modulation of high-frequency oscillating potentials in auditory cortex. Nature 383: 78-81

Bibbig, A.1999. gamma-beta transition, pattern separation and the plasticity of inhibitory and excitatory synapses. Soc. Neurosci. Abs.

Bracci, E, Vreugdenhil, M, Hack, S. P. & Jefferys, J. G. R. 1999. On the synchronising mechanisms of tetanically-induced hippocampal oscillations. J. Neurosci. In press.

Buhl E. H., Han Z-S., Lorinczi Z., Stezhka V. V. , Karnup S. V. & Somogyi P. 1994. Physiological properties of anatomically identified axo-axonic cells in the rat hippocampus. J Neurophysiol 71:1289-1307.

Buhl E. H., Szilagyi T., Halasy K. & Somogyi P. 1996. Physiological properties of anatomically identified basket and bistratified cells in the CA1 area of the rat hippocampus in vitro. Hippocampus 6:294-305.

Buhl, E.H., Tamas, G. & Fisahn, A. 1998. Cholinergic activation and tonic excitation induce persistent gamma oscillations in mouse somatosensory cortex in vitro. J. Physiol. 513:117-126.

Burchell, T. R., Faulkner, H. J. & Whittington, M. A. 1998. Gamma frequency oscillations gate temporally coded afferent inputs in the rat hippocampal slice. Neurosci. Lett. 255, 151-154.

Buzsáki, G. 1986. Hippocampal sharp waves: their origin and significance. Brain Res. 398, 242-52.

Chow, C. C., White, J. A., Ritt, J. & Kopell, N. 1998. Frequency control in synchronised networks of inhibitory neurons. J. Comput. Neurosci. 5: 407-420

Cobb S. R, Halasy K., Vida I., Nyiri G., Tamas G., Buhl E. H. & Somogyi P.. 1997. Synaptic effects of identified interneurons innervating both interneurons and pyramidal cells in the rat hippocampus. Neuroscience 79:629-48.

Cole, A. E. & Nicoll, R. A. 1984. Characterisation of a slow cholinergic post-synaptic potential recorded in vitro from rat hippocampal pyramidal cells. J. Physiol. 352: 173-188.

Colling, S. B., Stanford, I. M., Traub, R. D., & Jefferys, J. G. 1998. Limbic gamma rhythms. I. Phase-locked oscillations in hippocampal CA1 and subiculum. J. Neurophysiol. 80(1), 155-61.

Congar, P, Leinekugel, X., Ben-Ari, Y. & Crépel, V. 1997. A long-lasting calcium-activated nonselective cationic current is generated by synaptic stimulation or exogenous activation of group I metabotropic glutamate receptors in CA1 pyramidal neurons. J Neuroscience 17: 5366-5379.

Crook, S. M, Ermentrout, G. B. & Bower, J. M. 1998. Spike frequency adaptation affects the synchronization properties of networks of cortical oscillators, Neural Comput. 10:837-854.

Davies, C. H., Clarke, V. R., Jane, D. E. & Collingridge, G. L. 1995. Pharmacology of postsynaptic metabotropic glutamate receptors in rat hippocampal CA1 pyramidal neurones. Brit. J. Pharmacol. 116(2): 1859-69.

Ermentrout, G. B. & Kopell, N. 1998. Fine structure of neural spiking and synchronisation in the presence of conduction delays. Proc. Natl. Acad. Sci. 95: 1259-1264.

Faulkner, H. J., Traub, R. D. & Whittington, M. A. 1998. Disruption of synchronous gamma oscillations in the rat hippocampal slice: A common mechanism of anaesthetic drug action. Brit. J. Pharmacol. 125: 483-492.

Faulkner, H. J. Traub, R. D. & Whittington, M. A. 1999. Anaesthetic/amnesic agents disrupt beta frequency oscillations associated with potentiation of excitatory synaptic potentials in the rat hippocampal slice. Brit. J. Pharmacol. Submitted.

Fisahn, A., Pike, F. G, Buhl, E. H. & Paulsen, O. 1998. Cholinergic induction of network oscillations at 40 Hz in the hippocampus in vitro. Nature 394: 186-189.

Funahashi, M. & Stewart, M. 1998. Properties of gamma-frequency oscillations initiated by propagating poulation bursts in retrohippocampal regions of rat brain slices. J. Physiol. 510: 191-208

Gerstner, W., van Hemmen, J. L. & Cowen, J. 1996. What matters in neuronal locking?, Neural Comput. 8: 1653-1676.

Gray, C. M. & McCormick, D. A. 1996. Chattering cells: superficial pyramidal neurons contributing to the generation of synchronous oscillations in the visual cortex. Science 274: 109-113.

Guerineau, N. C., Bossu, J. L., Gahwiler, B. H. & Gerber, U. 1997. G-protein mediated desensitisation of metabotropic glutamatergic and muscarinic responses in CA3 cells in rat hippocampus. J. Physiol. 500: 487-496.

Gulyas, A. I., Hajos, N., Freund, T. F. 1996. Interneurons containing calretinin are specialized to control other interneurons in the rat hippocampus. J Neurosci 16:3397-411.

Jensen, K., Jensen, M. S. & Lambert, J. D. C. 1999. Post-tetanic potentiation of GABAergic IPSCs in cultured rat hippocampal neurones. J. Physiol. 519: 71-84.

Katsumaru, H., Kosaka, T., Heizmann, C. W. & Hama, K. 1988. Immunocytochemical study of GABAergic neurons containing the calcium-binding protein parvalbumin in the rat hippocampus. Exp Brain Res 72:347-362.

Kopell N, Ermentrout GB, Whittington MA, Traub RD 2000. Gamma rhythms and beta rhythms have different synchronization properties. Proc. Natl. Acad. Sci. 97(4):1867-72

Leung, L. S. 1996. Recurrent inhibition model of hippocampal CA1 in vivo. Trends Neurosci. 19: 468-470.

MacDonald, K. D., Fifkova, E., Jones, M. S. & Barth, D. S. 1998. Focal stimulation of the thalamic reticular nucleus induces focal gamma waves in cortex. J. Neurophysiol. 79: 474-477.

MacIver, M. B., Tanelian, D. L. & Mody, I. 1991. Two mechanisms for anesthetic-induced enhancement of GABA_A-mediated neuronal inhibition. Ann. N.Y. Acad. Sci. 625: 91-96.

McBain, C. J., DiChiara, T. J. & Kauer, J. A. 1994. Activation of metabotropic glutamate receptors differentially affects two classes of hippocampal interneurons and potentiates excitatory synaptic transmission. J. Neurosci. 14: 4433-4445.

McBain, C.J. Freund, T. F. & Mody, I. 1999. Glutamatergic synapses onto hippocampal interneurons: precision timing without lasting plasticity. Trends Neurosci. 22: 228-235.

Miles, R. & Wong, R. K. S. 1986. Excitatory synaptic interactions between CA3 neurones in the guinea-pig hippocampus. J. Physiol. 373: 397-418.

Miles, R. 1990. Variation in strength of inhibitory synapses in the CA3 region of guinea-pig hippocampus in vitro. J. Physiol. 431: 659-676.

Nunzi, M. G., Gorio, A., Milan, F., Freund, T. F., Somogyi, P. & Smith A. D. 1985. Cholecystokinin-immunoreactive cells form symmetrical synaptic contacts with pyramidal and nonpyramidal neurons in the hippocampus. J Comp Neurol 237:485-505.

Patrylo, P. R., Schweitzer, J. S. & Dudek, F. E. 1994. Potassium-dependent prolonged field bursts in the dentate gyrus: effects of extracellular calcium and amino acid receptor antagonists. Neuroscience 61: 13-19.

Pinault, D. & Deschênes, M. 1992. Voltage-dependent 40-Hz oscillations in rat reticular thalamic neurons in vivo. Neuroscience 51: 245-258.

Schmidt, K. E., Kim, D. S., Singer, W, Bonhoeffer, T. & Lowel, S. 1997. Functional specificity of long-range intrinsic and interhemispheric connections in the visual cortex of strabismic cats. J. Neurosci. 17:5480-5480.

Segal, M & Barker, J. L. 1984. Rat hippocampal neurons in culture: voltage-clamp analysis of inhibitory synaptic connections. J. Neurophysiol. 52: 469-87.

Siarey, R. J., Andreasen, M. & Lambert, J. D. C. 1995. Serotoninergic modulation of excitability in area CA1 of the in vitro rat hippocampus. Neurosci. Lett 199:211-214.

Singer, W. & Gray, C. M. 1995. Visual feature integration and the temporal correlation hypothesis. Annual Rev. Neurosci. 18: 555-586.

Sik et al., 1995. Hippocampal CA1 interneurons: an in vivo intracellular labelling study. J. Neurosci. 15: 6651-6665.

Steriade, M., Curró Diossi, R. & Contreras, D. 1993. Electrophysiological properties of intralaminar thalamocortical cells discharging rhythmic (40 Hz) spike-bursts at c.1000 Hz during waking and rapid eye movement sleep. Neuroscience 56: 1-9.

Steriade, M., Contreras, D., Amzica, F. & Timofeev, I. 1996. Synchronization of fast (30-40 Hz) spontaneous oscillations in intrathalamic and thalamocortical networks. J. Neurosci. 16: 2788-808.

Tallon Baudry, C., Bertrand, O., Delpuech, C. & Permier, J. 1997. Combined EEG and MEG recordings of visual 40 Hz responses to illusory triangles in humans. Neuroreport 8: 1103-1105.

Tamas, G., Somogyi, P. & Buhl, E. H. 1998. Differentially interconnected networks of GABAergic interneurons in the visual cortex of the cat. J Neurosci 18:4255-70.

Terman, D., Kopell, N. & Bose, A. 1998. Dynamics of two mutually coupled slow inhibitory neurons. Physica D. 117: 241-275.

Teschemacher, A., Zeise, M. L., Holsboer, F. & Zieglgansberger, W. 1995. The neuroactive steriod 5-alpha-tetrahydrodeoxycorticosetrone increases GABAergic postsynaptic inhibition in rat neocortical neurons in vitro. J. Neuroendocrinol. 7: 223-240.

Thomson, A. M., Girdlestone, D. & West, D. C. 1988. Voltage-dependent currents prolong single-axon postsynaptic potentials in LIII pyramidal cells in rat neocortical slices. J. Neurophysiol. 60: 1869-1907

Thomson, A. M. & Radpour, S. 1991. Excitatory connections between CA1 pyramidal cells revealed by spike triggered averaging in slices of rat hippocampus are partially NMDA receptor mediated. Eur. J. neurosci. 3: 587-601.

Traub, R. D., Whittington, M. A., Colling, S. B., Buzsáki, G. & Jefferys, J. G. R. 1996a. Analysis of gamma rhythms in the rat hippocampus in vitro and in vivo. J. Physiol. 493: 471-484.

Traub, R. D., Whittington, M. A., Stanford, I. M. & Jefferys, J. G. R. 1996b. A mechanism for generation of long-range synchronous fast oscillations in the cortex. Nature 383: 621-624.

Traub, R. D., Jefferys, J. G. & Whittington, M. A. 1997. Simulation of gamma rhythms in networks of interneurons and pyramidal cells. J. Comput. neurosci. 4: 141-150.

Traub, R. D., Whittington, M. A. & Jefferys, J. G. R. (1997). Gamma oscillation model predicts intensity coding by phase rather than frequency. Neural Computation 9, 1251-1264.

Traub, R. D., Schmitz, D., Jefferys, J. G. R. & Draguhn, A. 1999. High-frequency population oscillations are predicted to occur in hippocampal pyramidal neuronal networks interconnected by axoaxonal gap junctions. Neuroscience 92: 407-426.

Traub, R. D., Whittington, M. A., Buhl, E. H., Jefferys, J. G. R. & Faulkner, H. J. 1999. On the mechanism of the - frequency shift in neuronal oscillations induced in rat hippocampal slices by tetanic stimulation. J.Neurosci. 19: 1088-1105.

van Vreeswijk, C., Abbott, L. F. & Ermentrout, G. B. 1994. When inhibition not excitation synchronizes neural firing J. Comput. Neurosci.1: 313-322.

von Stein, A., Rappelsberger, P., Sarnthein, J. & Petsche, H. 1999. Synchronization between temporal and parietal cortex during multimodal object processing in man. Cerebral cortex, 9: 137- 150.

Wan, Q., Xiong, Z. G., Man, H. Y., Ackerley, C. A., Braunton, J., Lu, W. Y., Becker, L. E., MacDonald, J. F. & Wang, Y. T. 1997. Recruitment of functional GABA_A receptors to postsynaptic domains by insulin. Nature 388: 686-690.

Wang, X-J & Buzsáki, G. 1996. Gamma oscillation by synaptic inhibition in a hippocampal interneuron network model. J. Neurosci. 16: 6402-6413.

Wang, X-J, & Rinzel, J. 1993. Spindle rhythmicity in the reticularis thalami nucleus: synchronisation among mutually inhibitory neurons. Neuroscience 53: 899-904.

White, J. A., Chow, C. C., Ritt, J., Soto-Treviño, C. & Kopell, N. 1998. Synchronisation and oscillatory dynamics in heterogeneous, mutually inhibited neurons. J. Comput. Neurosci. 5:5-16.

Whittington, M. A., Traub, R. D. & Jefferys, J. G. R. 1995. Synchronised oscillations in interneuron networks driven by metabotropic glutamate receptor activation. Nature 373: 612-615.

Whittington, M. A., Jefferys, J. G. R. & Traub, R. D. 1996. Effects of intravenous anaesthetic agents on fast inhibitory oscillations in the rat hippocampus in vitro. Brit. J. Pharmacol. 118: 1977-1986.

Whittington, M. A., Stanford, I. M., Colling, S. B., Jefferys, J. G. R. & Traub, R. D. 1997a. Spatiotemporal patterns of gamma frequency oscillations tetanically induced in the rat hippocampal slice. J. Physiol. 502: 591-607.

Whittington, M. A., Traub, R. D., Faulkner, H. J., Stanford, I. M. & Jefferys, J. G. R. 1997b. Recurrent excitatory postsynaptic potentials induced by synchronised fast cortical oscillations. Proc. natl. Acad. Sci. 94: 12198-203.

Whittington, M. A., Traub, R. D., Faulkner, H. J., Jefferys, J. G. R. & Chettiar, K. (1998). Morphine disrupts long-range synchrony of gamma oscillations in hippocampal slices. Proc. Natl. Acad. Sci. 95, 5807-5811.

Whittington, M. A., Faulkner, H. J., Doheny, H. C. & Traub, R. D. 1999. Neuronal fast oscillations as a target site for psychoactive drugs. Pharmacology & Therapeutics. In press.

Figure 1. Types of oscillator involved in generating synchrony. A. Diagrams illustrating possible network configurations for EEG synchronisation. Neurons are represented underlying dura, skull and scalp. Dark circles = excitatory neurons, Gray stars = interneurons (or pacemaker neurons). Two main configurations have been shown: Pacemaker driven synchronous oscillations involve concurrent synaptic representation of intrinsic activity in a pacemaker neuron. This neuron can be present outside the neocortex or within it. Also, in the absence of pacemaker activity, network properties within the neo and archicortex can generate synchronous oscillatory activity too. It is likely that all three mechanisms illustrated combine to produce the complex patterns of synchronisation seen in the thalamocortical system in vivo (Steriade et al., 1996). However, in the archicortex no intrinsic pacemaker neurons (with frequencies within the gamma band) have been found. B. Stylised representation of the patterns of synchrony seen with the above mechanisms. Remote pacemaker activity will result in synchronous activity in the target population assuming approximately equal conduction times for axonal collateral branches. A fixed phase angle will be present between the target population and the pacemaker neuron. This situation will also arise, but with smaller fixed phase angles, for local pacemaker activity. Network generators (with no pacemaker neurons) of the type described here result in little or no phase angle between excitatory and inhibitory neurons. Combination of network and pacemaker activity may also alleviate fixed phase angles between elements of the oscillating population. [JPEG]

Figure 2. The principle behind inhibition-based oscillations. A. Stylised representation of the membrane potential response in two inhibitory interneurons connected via GABA_A receptor-mediated synaptic activity. If one interneuron is depolarised a high frequency train of action potentials (>100 Hz) is generated in that interneuron. These action potentials produce a temporally summating train of IPSPs in the non-depolarised interneuron. If both interneurons are concurrently depolarised then both fire action potentials synchronously and at gamma frequencies. This is a consequence of the mutual inhibition between the two neurons. The highest probability of action potential generation in both neurons is at the end of the decay phase of the IPSP (c. 25 ms after the initial action potential). As an action potential in one interneuron will prevent an action potential in the other, as the IPSP arrives, the most favourable time for the second interneuron to fire is concurrently with the first. Thus an inhibitory network of this configuration generates synchronous gamma frequency oscillations as an emergent property. B. Examples of the two firing patterns. The gray line shows the high-frequency firing in one depolarised interneuron. The black line shows the pattern of firing in this neuron if a population of interconnected interneurons are concurrently depolarised. [JPEG]

Figure 3. Example population and neuronal responses during ING. Pressure ejection of glutamate to area CA1 of the hippocampus, in the presence of ionotropic receptor blockers (R-CPP and NBQX) and GABA_B receptor blockers generates a locally synchronous gamma oscillation. The stratum pyramidale field potential (population response) shows a small oscillatory component with regular small population spikes at c25 ms intervals. Excitatory neuronal voltage (membrane potential) response shows a rhythmic train of hyperpolarising IPSPs. NB action potential generation is blocked in this example with intracellular perfusion of QX314. Interneuron responses show small amplitude trains of inhibitory potentials and regular action potential generation at gamma frequencies. Scale bars 1 mV (population), 4 mV (excitatory neuron), 20 mV (inhibitory neuron), 100 ms. Traces were not concurrently recorded. [JPEG]

Figure 4. Pharmacological manipulation of ING Recordings show the transmembrane current responses in excitatory pyramidal neurons (in the hippocampus) in the experimental conditions described in fig. 3. In the absence of drugs (normal condition) gamma is manifest as a train of outward synaptic currents (IPSCs) mediated by GABA_A receptor activation. Diazepam (500 nM) increases the amplitude of each IPSC with comparably little effect on decay kinetics. The resulting frequency of the IPSC train is approximately halved. Thiopental (20 µM) increases the decay kinetics of the IPSCs with a lesser effect on amplitude. Again frequency is approximately halved. Morphine (50 µM) has the opposite effect to these two drugs. IPSC amplitude is markedly decreased and oscillation frequency doubles. Scale bars 0.5 nA, 100 ms. [JPEG]

Figure 5. Example population and neuronal responses during PING (tetanus-induced). Pyramidal/interneuron network gamma was induced by brief tetanic stimulation of area CA1 of the hippocampus. The field potential (population response) shows a small oscillatory component with regular population spikes at c.25 ms intervals (NB population spikes are much larger than during ING (fig 3.). Excitatory neuronal voltage (membrane potential) response shows a rhythmic train of hyperpolarising IPSPs and AHPs. Interneuron responses show small amplitude trains of inhibitory potentials and regular action potential generation at gamma frequencies. Scale bars 1 mV (population), 4 mV (excitatory neuron), 20 mV (inhibitory neuron), 100 ms. Traces were not concurrently recorded. [JPEG]

Figure 6. Example population and neuronal responses during population gamma (glutamate-induced). As with ING (fig. 3) the field potential (population response) shows a small oscillatory component with regular small population spikes at c25 ms intervals. Excitatory neuronal voltage (membrane potential) response shows a rhythmic train of hyperpolarising IPSPs. Action potentials occur in 20% of periods of this inhibition-based rhythm on average. Interneuron responses show small amplitude trains of inhibitory potentials and regular action potential generation at gamma frequencies. Scale bars 1 mV (population), 4 mV (excitatory neuron), 20 mV (inhibitory neuron), 100 ms. Traces were not concurrently recorded. [JPEG]

Figure 7. Example population and neuronal responses during population gamma (pharmacologically induced). The population oscillation has little discernible population spike component (cf previous eg figures). Excitatory neurons demonstrate the trains of IPSPs that characterise inhibition-based rhythms but fire action potentials on only 5% of periods. Interneuronal responses show a clear AHP/IPSP component between each action potential and. as with the previous examples, fire single or double action potentials on almost every period. Scale bars 1 mV (population), 10 mV (excitatory neuron), 20 mV (inhibitory neuron), 100 ms. Traces from excitatory and inhibitory neurons were concurrently recorded. [JPEG]

Figure 8. Example population and neuronal responses during slow gamma. Gamma oscillations were generated by tetanic stimulation (as in fig. 5). Bath application of 20 µM thiopental reduced the oscillation frequency from 48 Hz to the 18 Hz (beta) rhythm shown. The population response is identical to that seen in normal PING but with an approximately half the frequency of population spike generation. Excitatory neurons show larger longer IPSPs between spikes as do inhibitory interneurons. Scale bars 1 mV (population), 4 mV (excitatory neuron), 20 mV (inhibitory neuron), 100 ms. Traces were not concurrently recorded. [JPEG]

Figure 9. Example population and neuronal responses during beta (with missed gamma beats). Gamma oscillations (PING) were generated by tetanic stimulation at two sites in hippocampal area CA1. The gamma rhythm transformed into a beta rhythm (see text) accompanied by an increase in the amplitude of post-spike AHPs and recurrent EPSPs. The population response shows a small, subthreshold gamma component but population spikes are generated at beta frequencies (ie synchronous excitatory neuronal discharges on only every 2^nd to 4^th subthreshold period. This phenomenon of ‘missed beats’ is demonstrated more clearly by the excitatory neuronal voltage response, Here the train of IPSPs at gamma frequencies is clearly visible and action potentials (with large AHPs cf previous example figures) occur on every 3^rd period. Interneuron recordings show action potential generation continuing at a fundamental gamma frequency but with occasional bursts of action potentials. Scale bars 1 mV (population), 4 mV (excitatory neuron), 20 mV (inhibitory neuron), 100 ms. Traces were not concurrently recorded. [JPEG]

Figure 10. The transition from PING to population gamma to ING in an excitatory pyramidal neuron. A. The recording shows the membrane voltage response in a hippocampal excitatory neuron to tetanic stimulation. The initial response shows PING (black bar #1), with the neuron firing on each period of a gamma-frequency oscillation. As the oscillation continues action potentials do not fire on each subthreshold period and are associated with a larger AHP (black bar #2). Finally spiking ceases and ING only is seen. B. Expanded epochs of the recording in A. showing the effect of enhanced AHP on the ability of the neuron to follow the gamma rhythm. Scale bars 50 mV (A), 5 mv (B), 400 ms (A), 25 ms (B). [JPEG]