



Next: About this document
Up: No Title
Previous: Contents
From the basic definitions, differential topology studies the global
properties of smooth manifolds, and differential geometry studies both
local properties (curvature) and global properties (geodesics). This
text studies how differential operators on a smooth manifold reveal
deep relationships between the geometry and the topology of the
manifold. This is a broad and active area of research, and
has been treated in
advanced research monographs such as [],
[], [].
This book in contrast is aimed at
students knowing just the basics of smooth manifold theory, say
through Stokes' theorem for differential forms. In particular, the
text assumes no knowledge of
differential geometry.
The goal of the text is to provide a thorough overview of
central topics in analysis on manifolds through the study of Laplacian
type operators on manifolds. The main subjects covered are Hodge
theory, heat operators for Laplacians on forms, and the
Chern-Gauss-Bonnet theorem in detail. Atiyah-Singer index
theory and zeta functions for Laplacian type operators are also
covered, although with less detail. The main technique used is the
heat flow associated to a Laplacian type operator. The
text can be taught in a one year course, and by the conclusion the
student should have an understanding of current research interests
in the field.
We now give a brief, quasi-historical overview of these topics,
followed by an outline of the book's organization.
The only natural differential operator on a manifold is the exterior
derivative d taking k-forms to 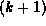 -forms. This operator is
defined purely in terms of the smooth structure. Using d, we can
define de Rham cohomology groups, the Euler characteristic and the
degree of a map of smooth manifolds, all of which give topological
information []. With some more work, we can
reformulate intersection theory in terms of integration of closed
forms [], and so in principle determine the entire real
cohomology ring of the manifold.
-forms. This operator is
defined purely in terms of the smooth structure. Using d, we can
define de Rham cohomology groups, the Euler characteristic and the
degree of a map of smooth manifolds, all of which give topological
information []. With some more work, we can
reformulate intersection theory in terms of integration of closed
forms [], and so in principle determine the entire real
cohomology ring of the manifold.
Once we enter the domain of differential geometry by introducing a
Riemannian metric on the manifold, we find a series of differential
operators associated to the metric, namely the Laplacians  on k-forms. In particular, the Laplacian on functions generalizes
the usual Laplacians on
on k-forms. In particular, the Laplacian on functions generalizes
the usual Laplacians on 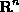 and on the circle. On a compact
manifold, the spectrum of these Laplacians contains both topological
and geometric information. In particular, by the Hodge theorem the
dimension of the kernel of
and on the circle. On a compact
manifold, the spectrum of these Laplacians contains both topological
and geometric information. In particular, by the Hodge theorem the
dimension of the kernel of 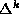 equals the
equals the 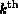 Betti
number (and so the Laplacians determine the Euler characteristic
Betti
number (and so the Laplacians determine the Euler characteristic
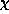 ).
).
The geometric information contained in 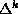 is more difficult to
extract. We consider the heat equation
is more difficult to
extract. We consider the heat equation 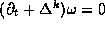 on k-forms with solution given by the heat semigroup
on k-forms with solution given by the heat semigroup
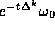 ,
, 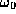 being the initial k-form. The
behavior of the trace of the heat semigroup as
being the initial k-form. The
behavior of the trace of the heat semigroup as 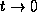 is controlled
by an infinite sequence of geometric data, starting with the volume of
the manifold and the integral of the scalar curvature. This is
surprising, since the trace is constructed just from the spectrum of
is controlled
by an infinite sequence of geometric data, starting with the volume of
the manifold and the integral of the scalar curvature. This is
surprising, since the trace is constructed just from the spectrum of
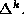
Now the kernel of 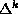 controls the behavior of
controls the behavior of
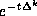 as
as 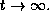 It turns out that the sum
It turns out that the sum 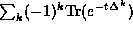 of the traces of the heat kernels is
independent of t. The long time behavior of this sum equals
by the Euler characteristic, while the short time behavior is given by
an integral of a complicated curvature expression.
of the traces of the heat kernels is
independent of t. The long time behavior of this sum equals
by the Euler characteristic, while the short time behavior is given by
an integral of a complicated curvature expression.
If the dimension of the manifold M is two, this equaltiy of long and
short time behavior of the heat flow leads to the Gauss-Bonnet
theorem, 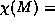
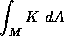 ,
where K is the Gaussian curvature and dA is the
area element. Note the remarkable fact that the integrand is
independent of the Riemannian metric. Of course, there are much
simpler proofs of Gauss-Bonnet, but this technique shows that a
generalization of Gauss-Bonnet exists in higher dimensions. The
explicit determination of the curvature integrand in this
generalization, originally due to Chern by other methods, is one of
the main results of the text. The proof is a modification of
techniques introduced by Getzler around 1985.
,
where K is the Gaussian curvature and dA is the
area element. Note the remarkable fact that the integrand is
independent of the Riemannian metric. Of course, there are much
simpler proofs of Gauss-Bonnet, but this technique shows that a
generalization of Gauss-Bonnet exists in higher dimensions. The
explicit determination of the curvature integrand in this
generalization, originally due to Chern by other methods, is one of
the main results of the text. The proof is a modification of
techniques introduced by Getzler around 1985.
The Chern-Gauss-Bonnet theorem, first shown around 1945, can itself be generalized. The Riemannian metric induces Hilbert space structures on the spaces of k-forms, and so d has an adjoint 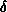 taking
taking 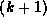 -forms to k-forms.
Recall that the index of an operator D on a Hilbert space is given by
-forms to k-forms.
Recall that the index of an operator D on a Hilbert space is given by
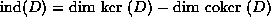 when the kernel and cokernel are finite dimensional.
From Hodge theory, we find that the index of the first order geometric operator
when the kernel and cokernel are finite dimensional.
From Hodge theory, we find that the index of the first order geometric operator 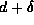 taking even forms to odd forms is just the Euler characteristic.
taking even forms to odd forms is just the Euler characteristic.
This suggests that we look for other geometrically defined
operators whose index is a topological invariant. One example is the
signature operator, whose index, the signature, is an important
topological quantity associated to the middle dimensional cohomology
of the manifold. The heat equation approach again gives the signature
as the integral of a curvature expression. Even more generally, the
Atiyah-Singer index theorem, dating from the early 1960s, shows that
the index of any elliptic first order geometric operator D
is given by such an integral, even though the index need not have an obvious topological interpretation. Thus we can state the Atiyah-Singer index theorem schematically as 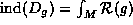 , where g denotes a Riemannian metric and
, where g denotes a Riemannian metric and 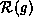 denotes the curvature expression.
denotes the curvature expression.
The index of these operators will be independent of the Riemannian metric, and so
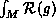 is also metric independent, as in the Gauss-Bonnet theorem. This implies that these particular curvature integrands are representatives of cohomology classes. As a result, Chern-Weil theory, which constructs representatives of certain cohomology classes from a Riemannian metric, naturally enters the picture.
is also metric independent, as in the Gauss-Bonnet theorem. This implies that these particular curvature integrands are representatives of cohomology classes. As a result, Chern-Weil theory, which constructs representatives of certain cohomology classes from a Riemannian metric, naturally enters the picture.
To summarize, the Gauss-Bonnet theorem equates the topological
quantity 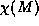 with the geometric quantity
with the geometric quantity 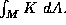 At the
end of the generalization process, the Atiyah-Singer index theorem
equates the analytic quantity
At the
end of the generalization process, the Atiyah-Singer index theorem
equates the analytic quantity 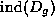 with a topological
quantity given by Chern-Weil theory. In fact, the index theorem
applies to all elliptic operators, not just geometrically defined
operators. This reinterpretation of the nature of both sides of the
index theorem indicates the depth of this theory.
with a topological
quantity given by Chern-Weil theory. In fact, the index theorem
applies to all elliptic operators, not just geometrically defined
operators. This reinterpretation of the nature of both sides of the
index theorem indicates the depth of this theory.
To see what lies beyond index theory, we go back to differential
topology and first ask what lies beyond cohomology. If the (twisted)
cohomology groups of a manifold vanish, a subtler or secondary
topological
invariant, the Reidemeister torsion, is well defined. In the 1970s,
concurrent with the development of the heat equation approach to index
theory, Ray and Singer proposed an analytic analogue of the Reidemeister
torsion defined from the Laplacians on k-forms. The definition
involves the zeta function of the Laplacian, which encodes the
spectrum of the Laplacian differently from the trace of the heat
operator. This analytic torsion was shown to equal the Reidemeister
torsion around 1980. We will show only that the analytic torsion is indeed
independent of the Riemannian metric, and so gives a smooth invariant
of the manifold.
Index theory and its offshoots continue to develop in many directions, including K-theory, operator theory, number theory and mathematical physics. (For example, in operator theory it is now considered hopelessly old fashioned to think of the index as an integer.) Hopefully, the readers of this book will contribute to this development.
In more detail, Chapter 1 treats the heat equation approach to Hodge
theory. We discuss heat flow for the Laplacian on 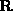 and the
circle. Riemannian metrics are defined, as are the associated Hilbert
spaces of k-forms. The Laplacians on forms are given in terms of
the Riemannian metric. After proving the basic analytic results
(Sobolev embedding theorem, Rellich compactness theorem), we give a
heat equation proof of the Hodge theorem, which gives an eigenform
decomposition of the Hilbert spaces of forms generalizing Fourier
series on the circle. This proof assumes the existence of an integral
kernel, the heat kernel, for heat flow for the
Laplacians on forms; the construction
of the heat kernel is in Chapter 3. The proof shows that the long
time behavior of the heat flow is controlled by the kernel of the
Laplacian. We then use Gårding's inequality to prove the standard
regularity results for the Laplacians and to give the Hodge
decomposition of the spaces of smooth forms. At this point the more
standard elliptic/potential theoretic proof of the Hodge theorem is
given in the exercises. We define the de Rham cohomology groups and
show that the kernel of the Laplacian on k-forms is isomorphic to
the k
and the
circle. Riemannian metrics are defined, as are the associated Hilbert
spaces of k-forms. The Laplacians on forms are given in terms of
the Riemannian metric. After proving the basic analytic results
(Sobolev embedding theorem, Rellich compactness theorem), we give a
heat equation proof of the Hodge theorem, which gives an eigenform
decomposition of the Hilbert spaces of forms generalizing Fourier
series on the circle. This proof assumes the existence of an integral
kernel, the heat kernel, for heat flow for the
Laplacians on forms; the construction
of the heat kernel is in Chapter 3. The proof shows that the long
time behavior of the heat flow is controlled by the kernel of the
Laplacian. We then use Gårding's inequality to prove the standard
regularity results for the Laplacians and to give the Hodge
decomposition of the spaces of smooth forms. At this point the more
standard elliptic/potential theoretic proof of the Hodge theorem is
given in the exercises. We define the de Rham cohomology groups and
show that the kernel of the Laplacian on k-forms is isomorphic to
the k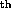 de Rham cohomology group. Thus the long time heat
flow is controlled by the topology of the manifold.
de Rham cohomology group. Thus the long time heat
flow is controlled by the topology of the manifold.
Chapter 2 covers just those parts of differential geometry needed to
construct the heat kernel. We introduce the various curvatures
associated to a Riemannian metric and prove that the Riemann curvature
tensor is the obstruction to a metric being locally flat. We define
the Levi-Civita connection for a Riemannian metric, and prove the
Bochner formula relating the Laplacian on forms to this connection and
the Riemannian curvature. The Bochner formula is proved using
supersymmetry/fermion calculus methods, and it leads to a quick proof
of Gårding's inequality used in Chapter 1. We then turn to the
study of geodesics and the exponential map, and give a technical
computation of the Laplacian on functions in Riemannian polar
coordinates.
In Chapter 3, we construct the heat kernel for the Laplacians on functions and forms. We use Duhamel's formula to motivate the complicated calculations. The construction shows that the short time behavior of the heat flow is determined by the geometry of the Riemannian metric. We also show that the heat kernel on functions is positive.
Chapter 4 discusses the heat equation approach to Atiyah-Singer index
theory. The main idea is to compare the long time and short time
information in the heat flows. We first show that the Euler
characteristic is given by an integral of a curvature expression
generalizing the Gauss-Bonnet theorem for surfaces. We then give a
fermion calculus proof of the Chern-Gauss-Bonnet theorem by showing
that the integrand is the expected Pfaffian of the curvature. There
is a
brief discussion of Chern-Weil theory, showing how
characteristic classes have representative forms constructed from the
curvature of a Riemannian metric. This allows us to give a precise
formulation of the Hirzebruch signature theorem. We do not prove this
theorem, as the fermion calculus is more involved, but refer the
reader to proofs in more advanced texts. We briefly discuss the
Hirzebruch-Riemann-Roch theorem; this discussion assumes familiarity
with complex geometry and can be omitted. (Since the Dirac operator
is even trickier to define and is treated extensively in
[], [], [], we do not
discuss it at all.) Finally, we define elliptic operators and state
the Atiyah-Singer index theorem.
In Chapter 5, we discuss the zeta function of the Laplacian on forms.
We show that the poles and special values
of the zeta function contain the same
information as the short time asymptotics of the heat kernel. For the
conformal Laplacian on functions, we show that 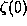 is a
conformal invariant given by a curvature expression, and that
is a
conformal invariant given by a curvature expression, and that
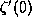 is a subtler conformal invariant. We then digress
to give Sunada's elegant construction of nonhomeomorphic manifolds
whose Laplacians on functions have the same spectrum.
is a subtler conformal invariant. We then digress
to give Sunada's elegant construction of nonhomeomorphic manifolds
whose Laplacians on functions have the same spectrum.
We define
Reidemeister and analytic torsion, which involves interpreting
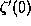 as the (logarithm of the) determinant of the
Laplacian. We show that analytic torsion is independent of the
Riemannian metric. We finish with a (not entirely self-contained)
discussion of the recent work of Bismut-Lott, which states precisely
in what sense analytic torsion arises as a secondary invariant when no
information is available from index theory techniques.
as the (logarithm of the) determinant of the
Laplacian. We show that analytic torsion is independent of the
Riemannian metric. We finish with a (not entirely self-contained)
discussion of the recent work of Bismut-Lott, which states precisely
in what sense analytic torsion arises as a secondary invariant when no
information is available from index theory techniques.
I would like to acknowledge the hospitality of Keio
University and the University of Warwick, where much of this text was
written. A special thanks is due to Tom Parker for allowing me to use
his proof of the Chern-Gauss-Bonnet theorem. I would also like to
acknowledge the support of the NSF and JSPS. A much different form of
support was provided by my wife, Sybil, and an extremely different
form by my children, Sam and Selene. This book is
dedicated to my family.




Next: About this document
Up: No Title
Previous: Contents
Steven Rosenberg
Fri Mar 29 15:36:16 EST 1996
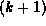 -forms. This operator is
defined purely in terms of the smooth structure. Using d, we can
define de Rham cohomology groups, the Euler characteristic and the
degree of a map of smooth manifolds, all of which give topological
information []. With some more work, we can
reformulate intersection theory in terms of integration of closed
forms [], and so in principle determine the entire real
cohomology ring of the manifold.
-forms. This operator is
defined purely in terms of the smooth structure. Using d, we can
define de Rham cohomology groups, the Euler characteristic and the
degree of a map of smooth manifolds, all of which give topological
information []. With some more work, we can
reformulate intersection theory in terms of integration of closed
forms [], and so in principle determine the entire real
cohomology ring of the manifold.




 on k-forms. In particular, the Laplacian on functions generalizes
the usual Laplacians on
on k-forms. In particular, the Laplacian on functions generalizes
the usual Laplacians on 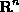 and on the circle. On a compact
manifold, the spectrum of these Laplacians contains both topological
and geometric information. In particular, by the Hodge theorem the
dimension of the kernel of
and on the circle. On a compact
manifold, the spectrum of these Laplacians contains both topological
and geometric information. In particular, by the Hodge theorem the
dimension of the kernel of 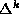 equals the
equals the 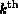 Betti
number (and so the Laplacians determine the Euler characteristic
Betti
number (and so the Laplacians determine the Euler characteristic
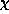 ).
).
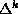 is more difficult to
extract. We consider the heat equation
is more difficult to
extract. We consider the heat equation 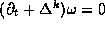 on k-forms with solution given by the heat semigroup
on k-forms with solution given by the heat semigroup
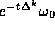 ,
, 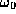 being the initial k-form. The
behavior of the trace of the heat semigroup as
being the initial k-form. The
behavior of the trace of the heat semigroup as 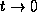 is controlled
by an infinite sequence of geometric data, starting with the volume of
the manifold and the integral of the scalar curvature. This is
surprising, since the trace is constructed just from the spectrum of
is controlled
by an infinite sequence of geometric data, starting with the volume of
the manifold and the integral of the scalar curvature. This is
surprising, since the trace is constructed just from the spectrum of
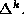
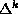 controls the behavior of
controls the behavior of
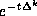 as
as 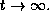 It turns out that the sum
It turns out that the sum 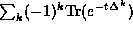 of the traces of the heat kernels is
independent of t. The long time behavior of this sum equals
by the Euler characteristic, while the short time behavior is given by
an integral of a complicated curvature expression.
of the traces of the heat kernels is
independent of t. The long time behavior of this sum equals
by the Euler characteristic, while the short time behavior is given by
an integral of a complicated curvature expression.
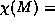
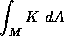 ,
where K is the Gaussian curvature and dA is the
area element. Note the remarkable fact that the integrand is
independent of the Riemannian metric. Of course, there are much
simpler proofs of Gauss-Bonnet, but this technique shows that a
generalization of Gauss-Bonnet exists in higher dimensions. The
explicit determination of the curvature integrand in this
generalization, originally due to Chern by other methods, is one of
the main results of the text. The proof is a modification of
techniques introduced by Getzler around 1985.
,
where K is the Gaussian curvature and dA is the
area element. Note the remarkable fact that the integrand is
independent of the Riemannian metric. Of course, there are much
simpler proofs of Gauss-Bonnet, but this technique shows that a
generalization of Gauss-Bonnet exists in higher dimensions. The
explicit determination of the curvature integrand in this
generalization, originally due to Chern by other methods, is one of
the main results of the text. The proof is a modification of
techniques introduced by Getzler around 1985.
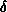 taking
taking 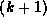 -forms to k-forms.
Recall that the index of an operator D on a Hilbert space is given by
-forms to k-forms.
Recall that the index of an operator D on a Hilbert space is given by
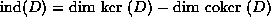 when the kernel and cokernel are finite dimensional.
From Hodge theory, we find that the index of the first order geometric operator
when the kernel and cokernel are finite dimensional.
From Hodge theory, we find that the index of the first order geometric operator 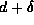 taking even forms to odd forms is just the Euler characteristic.
taking even forms to odd forms is just the Euler characteristic.
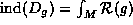 , where g denotes a Riemannian metric and
, where g denotes a Riemannian metric and 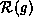 denotes the curvature expression.
denotes the curvature expression.
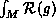 is also metric independent, as in the Gauss-Bonnet theorem. This implies that these particular curvature integrands are representatives of cohomology classes. As a result, Chern-Weil theory, which constructs representatives of certain cohomology classes from a Riemannian metric, naturally enters the picture.
is also metric independent, as in the Gauss-Bonnet theorem. This implies that these particular curvature integrands are representatives of cohomology classes. As a result, Chern-Weil theory, which constructs representatives of certain cohomology classes from a Riemannian metric, naturally enters the picture.
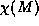 with the geometric quantity
with the geometric quantity 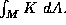 At the
end of the generalization process, the Atiyah-Singer index theorem
equates the analytic quantity
At the
end of the generalization process, the Atiyah-Singer index theorem
equates the analytic quantity 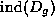 with a topological
quantity given by Chern-Weil theory. In fact, the index theorem
applies to all elliptic operators, not just geometrically defined
operators. This reinterpretation of the nature of both sides of the
index theorem indicates the depth of this theory.
with a topological
quantity given by Chern-Weil theory. In fact, the index theorem
applies to all elliptic operators, not just geometrically defined
operators. This reinterpretation of the nature of both sides of the
index theorem indicates the depth of this theory.
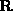 and the
circle. Riemannian metrics are defined, as are the associated Hilbert
spaces of k-forms. The Laplacians on forms are given in terms of
the Riemannian metric. After proving the basic analytic results
(Sobolev embedding theorem, Rellich compactness theorem), we give a
heat equation proof of the Hodge theorem, which gives an eigenform
decomposition of the Hilbert spaces of forms generalizing Fourier
series on the circle. This proof assumes the existence of an integral
kernel, the heat kernel, for heat flow for the
Laplacians on forms; the construction
of the heat kernel is in Chapter 3. The proof shows that the long
time behavior of the heat flow is controlled by the kernel of the
Laplacian. We then use Gårding's inequality to prove the standard
regularity results for the Laplacians and to give the Hodge
decomposition of the spaces of smooth forms. At this point the more
standard elliptic/potential theoretic proof of the Hodge theorem is
given in the exercises. We define the de Rham cohomology groups and
show that the kernel of the Laplacian on k-forms is isomorphic to
the k
and the
circle. Riemannian metrics are defined, as are the associated Hilbert
spaces of k-forms. The Laplacians on forms are given in terms of
the Riemannian metric. After proving the basic analytic results
(Sobolev embedding theorem, Rellich compactness theorem), we give a
heat equation proof of the Hodge theorem, which gives an eigenform
decomposition of the Hilbert spaces of forms generalizing Fourier
series on the circle. This proof assumes the existence of an integral
kernel, the heat kernel, for heat flow for the
Laplacians on forms; the construction
of the heat kernel is in Chapter 3. The proof shows that the long
time behavior of the heat flow is controlled by the kernel of the
Laplacian. We then use Gårding's inequality to prove the standard
regularity results for the Laplacians and to give the Hodge
decomposition of the spaces of smooth forms. At this point the more
standard elliptic/potential theoretic proof of the Hodge theorem is
given in the exercises. We define the de Rham cohomology groups and
show that the kernel of the Laplacian on k-forms is isomorphic to
the k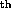 de Rham cohomology group. Thus the long time heat
flow is controlled by the topology of the manifold.
de Rham cohomology group. Thus the long time heat
flow is controlled by the topology of the manifold.
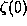 is a
conformal invariant given by a curvature expression, and that
is a
conformal invariant given by a curvature expression, and that
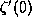 is a subtler conformal invariant. We then digress
to give Sunada's elegant construction of nonhomeomorphic manifolds
whose Laplacians on functions have the same spectrum.
is a subtler conformal invariant. We then digress
to give Sunada's elegant construction of nonhomeomorphic manifolds
whose Laplacians on functions have the same spectrum.
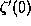 as the (logarithm of the) determinant of the
Laplacian. We show that analytic torsion is independent of the
Riemannian metric. We finish with a (not entirely self-contained)
discussion of the recent work of Bismut-Lott, which states precisely
in what sense analytic torsion arises as a secondary invariant when no
information is available from index theory techniques.
as the (logarithm of the) determinant of the
Laplacian. We show that analytic torsion is independent of the
Riemannian metric. We finish with a (not entirely self-contained)
discussion of the recent work of Bismut-Lott, which states precisely
in what sense analytic torsion arises as a secondary invariant when no
information is available from index theory techniques.