Research Theme

I am interested in the complex rhythms that arise in biological systems, and the mathematical problems that they generate. My research focuses on the development, implementation, and application of the theory of multi-scale dynamics to biological rhythms, including neural and cardiac signalling, and chemical oscillations. My research combines theoretical, numerical, and experimental methods.

  • Theoretical:   nonlinear dynamics, geometric singular perturbation theory, canard theory, bifurcation theory.
  • Numerical:   numerical continuation, invariant manifolds.
  • Experimental:   dynamic clamp (an experimental procedure that combines mathematical and electrophysiological techniques).

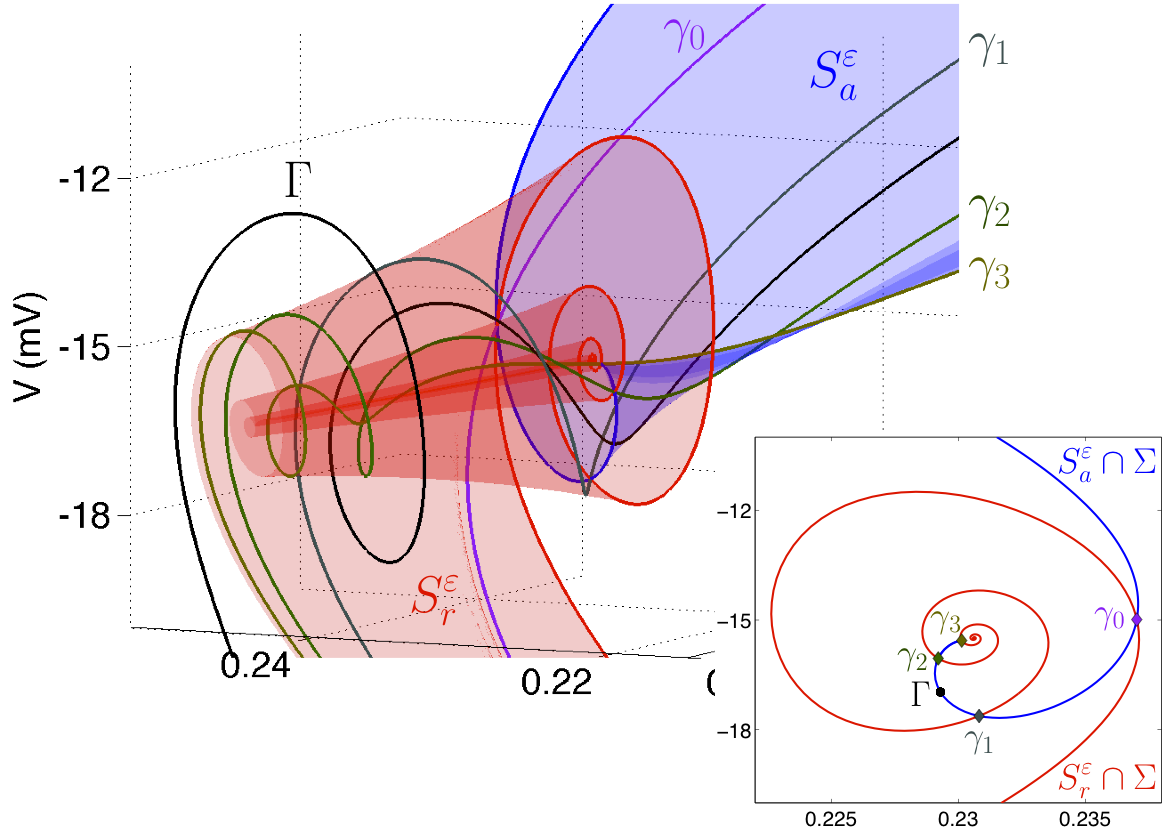
From data to modeling to analysis.

Current Interests

Slow/fast biological rhythms

Slow/fast rhythms are ubiquitous in nature. Rhythms I am currently interested in include the spiking/bursting activity of nerve and endocrine cells. The aim is to predict and control such behaviour in the interest of guiding experimental design.

Canard theory & its applications

Canard theory is a powerful mathematical framework that studies special solutions of slow/fast systems that delimit different dynamic regimes (in phase and parameter space). The identification, classification, and analysis of canard solutions is a rapidly growing area with significant and relevant applications.

Three time-scale systems

Geometric singular perturbation theory and canard theory are formulated for 2-timescale systems. Many biological phenomena evolve over more than 2-timescales. Results from the 2-timescale theory tend to break down in the 3-timescale context, and a proper theory needs to be developed.

Collaborators