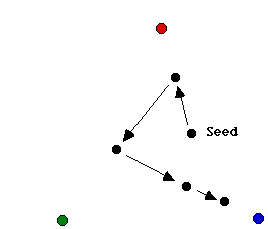
Fig.1. Playing the chaos game with rolls of red, green, blue, blue.
What Thomasina has discovered and what Valentine is trying to explain is what is now commonly called the "Chaos Game." The game proceeds in its simplest formulation as follows. Place three dots at the vertices of a triangle. Color the top vertex red, the lower left green, and the lower right blue. Then take a die and color two faces red, two green, and two blue.
To play the game, you need a seed, an arbitrary starting point in the plane. Starting with this point, the algorithm is: Roll the die, then depending upon which color comes up, move your point half the distance toward the appropriate colored vertex. Then iterate, i.e., repeat this process, using the terminal point of the previous move as the seed for the next. Do not plot the first 15 (or so) points generated by this algorithm, but after these few initial moves, begin to record each and every point. For example, Figure 1 shows the moves associated to rolling red, green, blue, and blue in order.

Fig.1. Playing the chaos game with rolls of red, green, blue, blue.
Provided that you have a browser that supports Java, you can play this game interactively on the web, courtesy of the Boston University Dynamical Systems and Technology Project. Click here to activate the game. The game "wakes up" with three vertices as above, though you can change this to play many other variations on the chaos game.
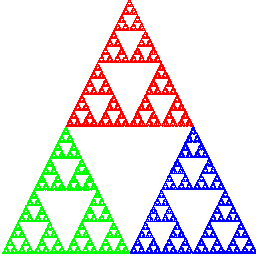
For leaf-making purposes, it is best to rework this algorithm in a slightly different form. Begin with a square in the plane, and put the red vertex in the center of the top side of the square, and the other two vertices at the lower vertices. The algorithm then linearly contracts all points in the original square into one of three smaller subsquares by moving half the distance toward the vertex in each subsquare. This can be visualized in Figure 2 as follows. Imagine what happens to the entire Sierpinski triangle as you contract toward each of the vertices. The result is the portion of the triangle colored red, green, or blue in that image.
 The Sierpinski Hexagon (Next Section)
The Sierpinski Hexagon (Next Section)
(Return to Dynamical Systems and Technology Home Page)