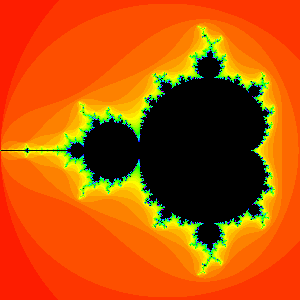
Figure 3. The Mandelbrot set
 3 Periods of the
Bulbs (Next Section)
3 Periods of the
Bulbs (Next Section) Fractal Geometry of the Mandelbrot Set
(Cover Page)
Fractal Geometry of the Mandelbrot Set
(Cover Page) 1 Iteration (Previous
Section)
1 Iteration (Previous
Section) BU Math Home Page
BU Math Home Page
The Mandelbrot set puts some geometry into the fundamental observation above. The precise definition is: The Mandelbrot set M consists of all of those (complex) c-values for which the corresponding orbit of 0 under x2 + c does not escape to infinity. From our previous calculations, it follows that c = 0, -1, -1.1, -1.3, -1.38, and i all lie in the Mandelbrot set, whereas c = 1 and c = 2i do not.
At this point, a natural question is: Why would anyone care about the fate of the orbit of 0 under x2 + c ? Why not the orbit of i ? Or 2 + 3i ? Or any other complex seeds, for that matter? As we will see below, there is a very good reason for inquiring about the fate of the orbit of 0; somehow the orbit of 0 tells us a tremendous amount about the fate of other orbits under x2 + c.
Before turning to this idea, note that the very definition of the Mandelbrot set gives us an algorithm for computing it. We simply consider a square in the complex plane (usually centered at the origin with sides of length 4). We overlay a grid of equally spaced points in this square. Each of these points is to be considered a complex c-value. Then, for each such c, we ask the computer to check whether the corresponding orbit of 0 goes to infinity (escapes) or does not go to infinity (remains bounded). In the former case, we leave the corresponding c-value (pixel) white. In the latter case, we paint the c-value black. Thus the black points in Figure 3 represent the Mandelbrot set.

Figure 3. The Mandelbrot set
Two points need to be made. Figure 3 is only an approximation of the Mandelbrot set. Indeed, it is not possible to determine whether certain c-values lie in the Mandelbrot set. We can only iterate a finite number of times to determine if a point lies in M . Certain c-values close to the boundary of M have orbits that escape only after a very large number of iterations.
A second question is: How do we know that the orbit of 0 under x2 + c
really does escape to infinity? Fortunately, there is an easy
criterion which helps:
The Escape Criterion: Suppose |c| is less than or equal to 2. If the orbit of 0 under x2 + c ever lands outside of the circle of radius 2 centered at the origin, then this orbit definitely tends to infinity.
It may seem that this criterion is not too valuable, as it only works when |c| is less than or equal to 2. However, it is known that the entire Mandelbrot set lies inside this disk, so these are the only c-values we need consider anyway.
 3 Periods of the Bulbs (Next Section)
3 Periods of the Bulbs (Next Section) Fractal Geometry of the Mandelbrot Set (Cover Page)
Fractal Geometry of the Mandelbrot Set (Cover Page) 1 Iteration (Previous Section)
1 Iteration (Previous Section) BU Math Home Page
BU Math Home Page