

Figure 4. Several decorations on the Mandelbrot set
 4 Filled Julia Sets (Next Section)
4 Filled Julia Sets (Next Section) Fractal Geometry of the Mandelbrot Set (Cover Page)
Fractal Geometry of the Mandelbrot Set (Cover Page) 2 The Mandelbrot Set (Previous Section)
2 The Mandelbrot Set (Previous Section) BU Math Home Page
BU Math Home Page
Note that the Mandelbrot set consists of many small decorations. Closer inspection of these decorations shows that all of them are different in shape.


Figure 4. Several decorations on the Mandelbrot set
For example, consider any decoration directly attached to the main cardioid in M. We call this bulb a primary bulb or decoration. This decoration in turn has infinitely many smaller decorations attached, as well as what appear to be antennas. In particular, as is clearly visible in Figure 4, the "main antenna" attached to each decoration seems to consist of a number of spokes which varies from decoration to decoration.
There is a beautiful relationship between the number of spokes on these antennas and the dynamics of x2 + c for c inside the primary bulb. It is known that if c lies in the interior of such a decoration, then the orbit of 0 is attracted to a cycle of a given period n. The number n is the same for any c inside this main decoration. (It is a multiple of n for c inside the other smaller decorations attached to the primary decoration.) For example, c = -1 and c = -1.1 both lie inside the largest primary bulb just to the left of the main cardioid. For these c-values, the orbit of 0 is attracted to a cycle of period 2.
At this point, it is useful to perform a series of computer experiments that yield the periods of some of the other primary decorations. You can easily check the following facts using a computer and any of a number of available software packages. (See, for example [9] or [12].)
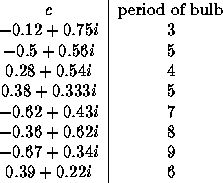
It is easy to check that M is symmetric about the real axis and that these periods hold for the complex conjugate c-values. This gives us a larger table of results. In Figure 5 we have summarized some of these results graphically.
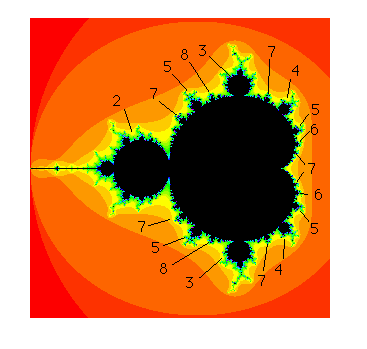
Figure 5. Periods of the primary bulbs in M
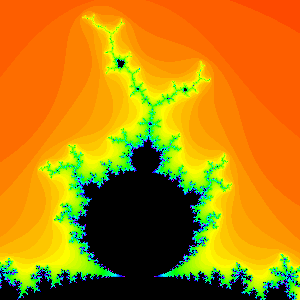
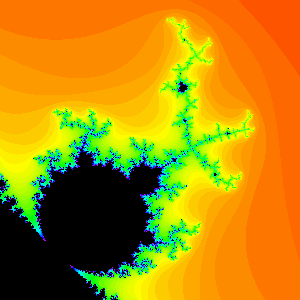
Further experimentation shows that there is a remarkable relationship between the number of spokes in the largest antenna attached to a primary decoration and the period of that decoration. These numbers are exactly the same! (Don't forget to count the spoke emanating from the primary decoration to the main junction point.) See Figure 6.
 Period 3 Bulb
Period 3 Bulb
 Period 4 Bulb
Period 4 Bulb
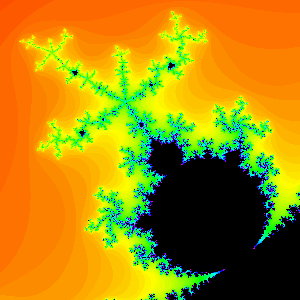 Period 5 Bulb
Period 5 Bulb
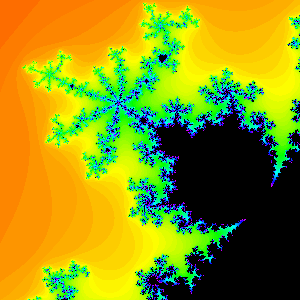 Period 7 Bulb
Period 7 Bulb
Figure 6. Note that the period of the bulb is the
same
as the number of spokes in the antenna
The following short quiz will help you develop your skills at recognizing the period of a bulb on the Mandelbrot Set.
 4 Filled Julia Sets (Next Section)
4 Filled Julia Sets (Next Section) Fractal Geometry of the Mandelbrot Set (Cover Page)
Fractal Geometry of the Mandelbrot Set (Cover Page) 2 The Mandelbrot Set (Previous Section)
2 The Mandelbrot Set (Previous Section) BU Math Home Page
BU Math Home Page