BU Math Home Page

4 Filled Julia Sets

There is a second, more dynamic way to calculate the periods of these primary bulbs in M. To explain this, we have to introduce the notion of a filled Julia set.

The filled Julia set for x² + c is subtly different from the Mandelbrot set. For M, we calculated only the orbit of 0 for each c-value and then displayed the result. A c-value lies in M if the corresponding orbit of 0 does not escape to infinity. Thus, M is a picture in the c-plane, the parameter plane.

For the filled Julia sets, we fix a c-value and then consider the fate of all possible seeds for that fixed value of c. Those seeds whose orbits do not escape form the filled Julia set of x² + c. Caution: There is also a notion of the Julia set. This term is used to describe the boundary of the filled Julia set.

Orbits that do escape do not lie in the filled Julia set. Thus we get a different filled Julia set of each different choice of c. That is, the filled Julia set is a picture in the dynamical plane, not the parameter plane. We denote the filled Julia set for x² + c by J_c. In Figure 7 we have displayed the filled Julia sets for a variety of c-values.

c = -1.037 + 0.17i in a period 2 bulb

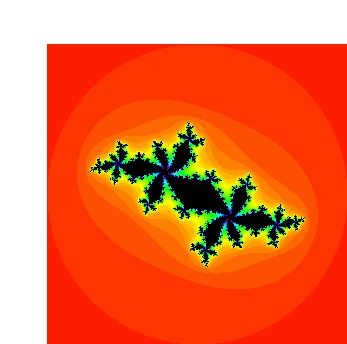
c = -0.52 + 0.57i in a period 5 bulb

c = 0.295 + 0.55i in a period 4 bulb

c = -0.624 + 0.435i in a period 7 bulb.

Figure 7. The filled Julia sets for several c-values

z₀ = r exp (it)

where t is the polar angle and r is the magnitude of z₀ But then the orbit of z₀ under x² is

z₀ = r exp (it)

z₁ = r² exp (i2t)

z₂ = r⁴ exp (i4t)

z₃ = r⁸ exp (i8t)

and so forth. The magnitude of z_n is r^{2^n}. Thus, the orbit of x₀ tends to infinity if r > 1 and to 0 if r < 1. If r = 1, the orbit of the seed remains trapped for all iterations on the unit circle.

It follows that any seed on or inside the circle of radius 1 centered at the origin has an orbit that does not escape to infinity. It therefore follows that J₀ consists of all those seeds whose orbits lie on or insider the unit circle centered at the origin.

Incidentally, the fate of orbits of x² that lie on the unit circle is quite an interesting story. These are precisely the orbits that behave in a chaotic fashion. See [3] for more details.

Other filled Julia sets are much more difficult to compute. To see them, we must use a computer. The algorithm is, of course, a direct consequence of the definition of J_c. We simply consider a grid of points centered at the origin and compute the orbit of each of these points under x² + c. Either this orbit tends to infinity (in which case the seed was not in J_c) or else the orbit does not (and so the seed lies in J_c).

The Mandelbrot set:

• is a picture in parameter space
• records the fate of the orbit of 0

The filled Julia set

• is a picture in dynamical plane
• records the fate of all orbits

BU Math Home Page