If you are viewing this page with Netscape, the blinking text indicates the corrections that should be made.

How to determine which printing you have: Three quarters of the way down the copyright page (which starts with the "GWO A Gary W. Ostedt Book" logo), there is the line

Below that line is a decreasing list of numbers. The last number in that list is the number of the printing that you have. For example,

indicates that you have the second printing.

Answer to Section 1.2, Exercise 11, Page 666:
The arbitrary constant k is "any positive real number."

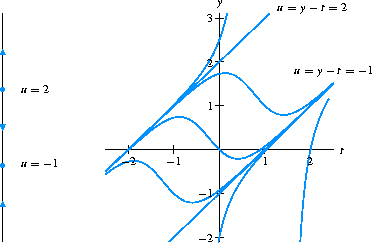
Answer to Section 1.4, Exercise 5, Page 669:
The vertical axis should be labeled with a w rather than with a y.

Section 1.6, Page 84:
Given the hypothesis of the Linearization Theorem, f'(y₀) exists. So the phrase "or if f'(y₀) does not exist" in the third bullet of the theorem is unnecessary.

Answers to Section 1.6, Exercises 27 and 29, Pages 671-672:
Since the directions indicate that y=0 is in the middle of the segment shown, the graphs cannot be translated left or right arbitrarily. Replace that phrase with " The following graph is one of many possible answers. "

Answer to Section 1.9, Exercise 5, Page 674:
The arrows point in the wrong direction on the phase line. Here is the correct figure:

Section 1.9, Exercise 24, Page 130:
In part (c), no interval about y=0 satisfies the inequality as stated. We meant to say "For what interval of y's near y=0 is 0.9|y| <= |-y + y^2/4| <= 1.1|y| ?

Section 2.1, Page 150:
The minus sign in the differential equation in the captions of both Figures 2.14 and 2.15 should be a plus sign. In other words, the differential equation should be

This should be the same differential equation as the one in the caption of Figure 2.16.

Section 2.1, Exercise 24, Page 155:
Part (a) uses the word spring where it really should say mass. Change the first sentence to read as follows:

Assuming that the only forces acting on the mass are the force due to gravity and the force of the spring, formulate two different (but related) second-order differential equations that describe the motion of the mass.

Section 2.3, Page 180:
The first line of the second display should be:

This typo was fixed in the second printing.

Answer to Section 3.1, Exercise 11(c), Page 684:
The horizontal axis should be labeled with the variable t, and the vertical axis should be labeled with the variables x and y.

Section 3.2, Page 239:
Near the top of the page, we give simultaneous equations for the eigenvalue 2. Although the equations that we give are correct, it is more natural to express the second equation as -6y=0 rather than -2y=0.

Figure 3.11, Page 246:
The horizontal axis should be labeled with the variable y, and the vertical axis should be labeled with the variable v.

Answer to Section 3.2, Exercise 25, Page 688:
The horizontal axis should be labeled with the variable y, and the vertical axis should be labeled with the variable v.

Section 3.3, Page 257:
In the third display on this page, the coefficient of -4 in the exponent should be -3. In other words, we should have

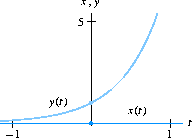
Answer to Section 3.3, Exercise 9, Page 689:
The x(t)- and y(t)-graphs for the initial condition (0,1) at the very bottom of the first column have the variable t heading in the wrong direction. Here are the correct graphs:

Section 3.4, Exercise 15, Pages 279 and 693:
Although it may not be clear to the reader with good eyesight, we intend for the amplitudes in graph (ii) on Page 279 to be decreasing at an exponential rate. Similarly, the amplitudes in graph (v) should be increasing at an exponential rate. On Page 693, we should say that the natural period for both graphs (ii) and (v) is 1.25 rather than exactly 1.

Section 3.5, Figure 3.38, Page 294:
We flipped the labels for x(t) and y(t) on the right-hand graph. Here is the figure with the correct labels:

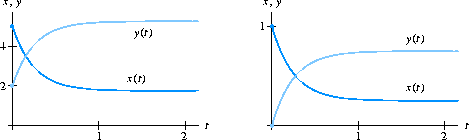
Section 3.5, Exercise 14, Page 296:
Suppose lambda is an eigenvalue...

Answer to Section 3.5, Exercise 19, Page 696:
In the answer to Part (f), we omitted a coefficient of 5 in the exponent of the exponential for the y(t) function. The exponent should be 5t rather than t.

Section 3.6, Pages 298-300:
At least we were consistent in flipping the coefficients in the "Free Gift" example! To fix this sequence of typos, interchange 7 and 10 throughout. (There are 10 occurrences of both.) The signs are correct as is.

If you want to take a look at corrected pages, we have them in gif format (which look lousy but are easy to display) or in postscript format (which look nice but require a postscript viewer such as ghostview to display).

Section 3.6, Page 303:
To be consistent with the definition in Section 3.4, the natural frequency is really omega/(2 pi). Omega (before it is divided by 2 pi) is often called the angular frequency.

Section 3.6, Page 307:
We dropped a minus sign the first time that we wrote the eigenvalue for the critically damped oscillator with m=1 and k=2 (in the middle of the page). It should be s=-sqrt(2). The rest of the discussion is correct as is.

Section 3.6, Page 308:
The formula for the period of an underdamped oscillator contained in the second bullet of the summary is missing a factor of m in the numerator. The period should be 4 m pi/sqrt(4 k m - b²).

Answer to Section 3.6, Exercise 11(b), Page 698:
The minus sign between the two terms in the solution should be a plus sign. In other words, the correct answer is

This typo was fixed in the second printing.

Section 3.8, Page 328:
When we defined the determinant, we messed up one of the subscripts. The correct formula is

Section 3.8, Page 329:
In this section, we seem to like to confuse the terms eigenvector and eigenvalue. In the middle of the next to last paragraph on the page, we should have written

Section 3.8, Page 335:
Same typo as on Page 329. About one-third of the way down the page, the paragraph should begin:

Section 4.2, Page 362:
We flipped the formulas for period and frequency in the last sentence of the first paragraph. That sentence should read:

Section 4.2, Page 367:
The sentence two-thirds of the way down the page that starts with "In order for" should read "In order for a e^(2 i t) to be a solution" That is, the exponent should be 2i t rather than simply i t.

Answers to Section 4.2, Page 703:
If you prefer reduced fractions in your answers, note that 48/320=3/20, 24/320=3/40, 17/85=1/5, 35/85=7/17, 30/85=6/17, 16/260=4/65, and 2/260=1/130.

Answer to Section 4.2, Exercise 15(b), Page 703:
We are missing a minus sign. The correct answer for A is

Section 4.3, Page 376:
We messed up a minus sign when we expanded y_c(t) at the bottom of the page. The correct expression for y_c(t) is

Section 4.3, Page 379:
Three lines up from Figure 4.20, we want the parameter omega to be very close to sqrt(2), rather than very close to t.

Hint for Section 4.3, Exercise 23, Page 704:
Replace T=3 with T=3/2.

Section 4.4, Page 387:
In the caption to Figure 4.22, the denominator should be enclosed in a square root sign. That is,

This typo was fixed in the second printing.

Section 4.4, Page 388:
When we convert the phase angle -pi/2 to degrees, we dropped the minus sign. This happens in the fourth line above Figure 4.25 as well as in the caption to Figure 4.25.

Answer to Section 4.4, Exercise 3, Page 704:
In part (a), there is NO -q term in the numerator of the partial of A with respect to w.

Also, the hint for part (b) is better expressed as "The critical points of A as a function of w satisfy either w=0 or w^2=q-p^2/2."

These changes were made in the second printing.

Section 4.4, Exercise 4, Page 390:
This exercise was seriously broken in the first printing. For the second and subsequent printings, it was replaced by:

For the function M(p,q) of Exercise 3,

1. for q=1, plot M(p,q) as a function of p,
2. explain why M(p,q)=1/sqrt(p^2 q - p^4/4) if the damping is small enough; and
3. explain why M(p,q) is proportional to 1/p as p goes to 0.

Section 5.1, Exercise 6, Page 418:
The coefficient of the xy-term in the equation for dy/dt should be -2 rather than -1.

Answer to Section 5.2, Exercise 13, Page 710:
There is NO equilibrium point at (0,2) contrary to what you see in the figures for parts (a) and (b).

Section 6.1, Page 500:
In the fourth line above the heading "Computation of Laplace Transforms of Exponential Functions," the text should read:

Section 6.2, Page 513:
The inverse Laplace transform of 2/(s+1) is 2e^(-t).

Section 6.2, Page 513:
In the third line below the heading "Shifting the Origin on the t-Axis," the text should read:

Section 6.2, Page 515:
In the third line, the text should read:

Answer to Section 6.2, Exercise 1, Page 715:
There is a minus sign missing from the exponent. In other words, the correct answer is (1-e^(-as))/s.

Section 6.3, Page 520:
There is an s missing in the second line of the display near the top of the page. That line should be

Section 6.3, Page 529:
An inverse sign on the right-most inverse Laplace transform is missing from the next-to-last displayed equation on this page.

Section 6.4, Page 537:
While deriving the closed-form solution using the Laplace transform, we multiplied 1 by 2 and got 1. Unfortunately the remainder of our derivation is based on this mistake. The mistake first arises in the third display down the page. That display should read:

Therefore the first of the two fractions in the next three displays should be

The solution therefore includes one more term than shown. In other words, the solution is

Appendix A, Page 650:
We interchanged the words "forced" and "unforced" in the first two sentences of the second paragraph under the heading "Linear Differential Equations." They should read:

If the right-hand side of a linear equation is zero (that is, r(t)=0) then the equation is called homogeneous or unforced. Otherwise it is said to be nonhomogeneous or forced.

These typos were fixed in the second printing of this edition.

Appendix A, Page 654:
In the middle of the page, we substitute yp(t)=a cos t + b sin t into the left-hand side of the differential equation and in the second of the three lines of the calculation we have sin t where cos t should be. In other words, the middle of the three equations should read:

= -a sin t + b cos t + 2a cos t + 2b sin t

The third line is correct as is.

Answer to Appendix A, Exercise 7, Page 724:
Take k=43/4 for the initial-value problem.

Answer to Appendix A, Exercise 9, Page 724:
There is nothing wrong with the answer given, but a more appropriate answer would be:

Tends to a solution that satisfies -1/2 < y(t) < 1.

Special thanks to David Arnold, Marina Bevzushenko, Roger Bingham, Brian Bradie, David Brown, Barbara Cavalieri, Richard J. Charnigo, Jr., Steve Clayton, Matt Corbo, Elwood Devaney (the true mathematical genius in the Devaney clan), David Dudley, Emily Edwards, Murray Eisenberg, Mark Farris, Greg Fredericks, Greg Glatt, Michael Hayes, Tyler Haynes, Ben Haytock, Stephen Hrutka, Mike Hurley, Vikram Kapur, Wally Lofaro, Tony Magni, Andres Martinez, Alejandro Montes, Justin Morgan, Kent Morrison, Mark Omodt, Wes Ostertag, Rhiannon Peasco, Steve Pennell, Paul Porch, Jenny Price, Avijit Purkayastha, Tom Read, Peggy Rejto, Jason Schlabach, Ann Sitomer, George Spencer, Phillip Straffin, Fritz Ward, and Bob Worth for pointing out errors to us.