For each player, let ![]() be the number of tournament games
the player has competed, or, for unrated players, the value
assigned from Step 1 of the algorithm.
Let
be the number of tournament games
the player has competed, or, for unrated players, the value
assigned from Step 1 of the algorithm.
Let ![]() be the player's pre-event rating, or, for unrated
players, the imputed rating assigned from Step 1.
Let
be the player's pre-event rating, or, for unrated
players, the imputed rating assigned from Step 1.
Let
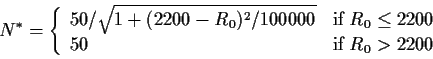 |
(1) |
Example: Suppose a player's pre-event rating is
![]() based on
based on ![]() games.
Then according to the formula above,
games.
Then according to the formula above,
N* = 50/sqrt(1 + (2200-1700)^2/100000) = 50/sqrt(3.5) = 26.7
Consequently, the value of ![]() is
the smaller of
is
the smaller of ![]() and
and ![]() , which is therefore
, which is therefore
![]() .
So the effective number of games for the player in
this example is
.
So the effective number of games for the player in
this example is ![]() .
.