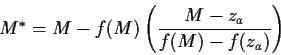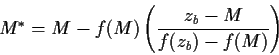This procedure is to be used for players with either ![]() ,
or players who have had either all wins or all losses in
all previous rated games.
,
or players who have had either all wins or all losses in
all previous rated games.
The algorithm described here extends the old provisional rating formula by ensuring that a rating does not decrease from wins or increase from losses. In effect, the algorithm finds the rating at which the attained score for the player equals the sum of expected scores, with expected scores following the ``provisional winning expectancy'' formula below. For most situations, the resulting rating will be identical to the old provisional rating formula. Instances that will result in different ratings are when certain opponents have ratings that are far from the player's initial rating. The computation to determine the ``special'' rating is iterative, and is implemented via a linear programming algorithm.
Define the ``provisional winning expectancy,'' ![]() , between
a player rated
, between
a player rated ![]() and his/her
and his/her ![]() -th opponent rated
-th opponent rated ![]() to be
to be
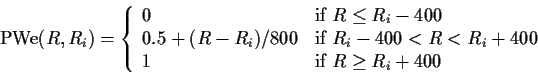
Let ![]() be the ``prior'' rating of a player
(either the pre-event rating for rated players, or the
Step 1 imputed rating for unrated players), and
be the ``prior'' rating of a player
(either the pre-event rating for rated players, or the
Step 1 imputed rating for unrated players), and ![]() be the
effective number of games.
Also let
be the
effective number of games.
Also let ![]() be the number of games in the current event,
and let
be the number of games in the current event,
and let ![]() be the total score out of the
be the total score out of the ![]() games
(counting each win as 1, each loss as 0, and each draw as
0.5).
games
(counting each win as 1, each loss as 0, and each draw as
0.5).
The variables ![]() and
and ![]() , which are the
adjusted initial rating and the adjusted score, respectively,
are used in the special rating procedure.
If a player has competed previously, and all the player's games were wins,
then let
, which are the
adjusted initial rating and the adjusted score, respectively,
are used in the special rating procedure.
If a player has competed previously, and all the player's games were wins,
then let
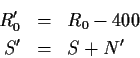
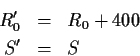
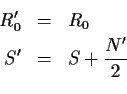
The objective function
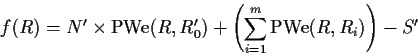
Let
![]() be a tolerance to
detect values different from zero.
Also, let
be a tolerance to
detect values different from zero.
Also, let ![]() ,
,
![]() , and, for
, and, for ![]() ,
,
![]() ,
, ![]() .
Denote the unique
.
Denote the unique ![]() and
and ![]() ,
, ![]() , as the
collection
, as the
collection