This algorithm is to be used for players with ![]() who have not had either all wins or all losses in
every previous rated game.
who have not had either all wins or all losses in
every previous rated game.
Define the ``Standard winning expectancy,'' ![]() , between
a player rated
, between
a player rated ![]() and his/her
and his/her ![]() -th opponent rated
-th opponent rated ![]() to be
to be
The value of ![]() , which used to take on the values 32, 24 or 16,
depending only on a player's pre-event rating,
is now defined as
, which used to take on the values 32, 24 or 16,
depending only on a player's pre-event rating,
is now defined as
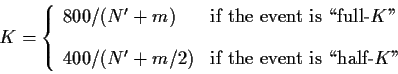
| Value of |
|||
| Full-K | Half-K | ||
| 6 | 4 | 80 | 50 |
| 6 | 6 | 66.67 | 44.44 |
| 6 | 10 | 50 | 36.36 |
| 20 | 4 | 33.33 | 18.18 |
| 20 | 6 | 30.77 | 17.39 |
| 20 | 10 | 26.67 | 16 |
| 50 | 4 | 14.81 | 7.69 |
| 50 | 6 | 14.29 | 7.54 |
| 50 | 10 | 13.33 | 7.27 |
If ![]() , or if the player competes against any opponent more
than twice,
the ``standard'' rating formula
that results in
, or if the player competes against any opponent more
than twice,
the ``standard'' rating formula
that results in ![]() is given by
is given by
If both ![]() and the player competes against no player
more than twice, then the ``standard'' rating formula
that results in
and the player competes against no player
more than twice, then the ``standard'' rating formula
that results in ![]() is given by
is given by
The resulting value of ![]() is the rating produced by the
``standard'' rating algorithm.
is the rating produced by the
``standard'' rating algorithm.