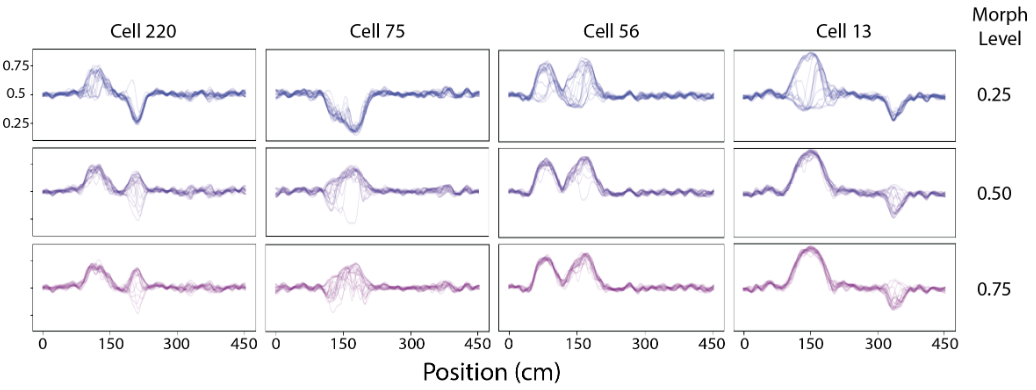
Estimating Fluctuations in Neural Representation of Uncertain Environments
I develop a new state-space modeling framework to address two important unsolved issues related to remapping. First, neurons may exhibit significant tria-to-trial or moment-to-moment variability in the firing patterns used to represent a particular environment or stimulus. Second, in ambiguous environments and tasks that involve cognitive uncertainty, neural populations may rapidly fluctuate between multiple representations.
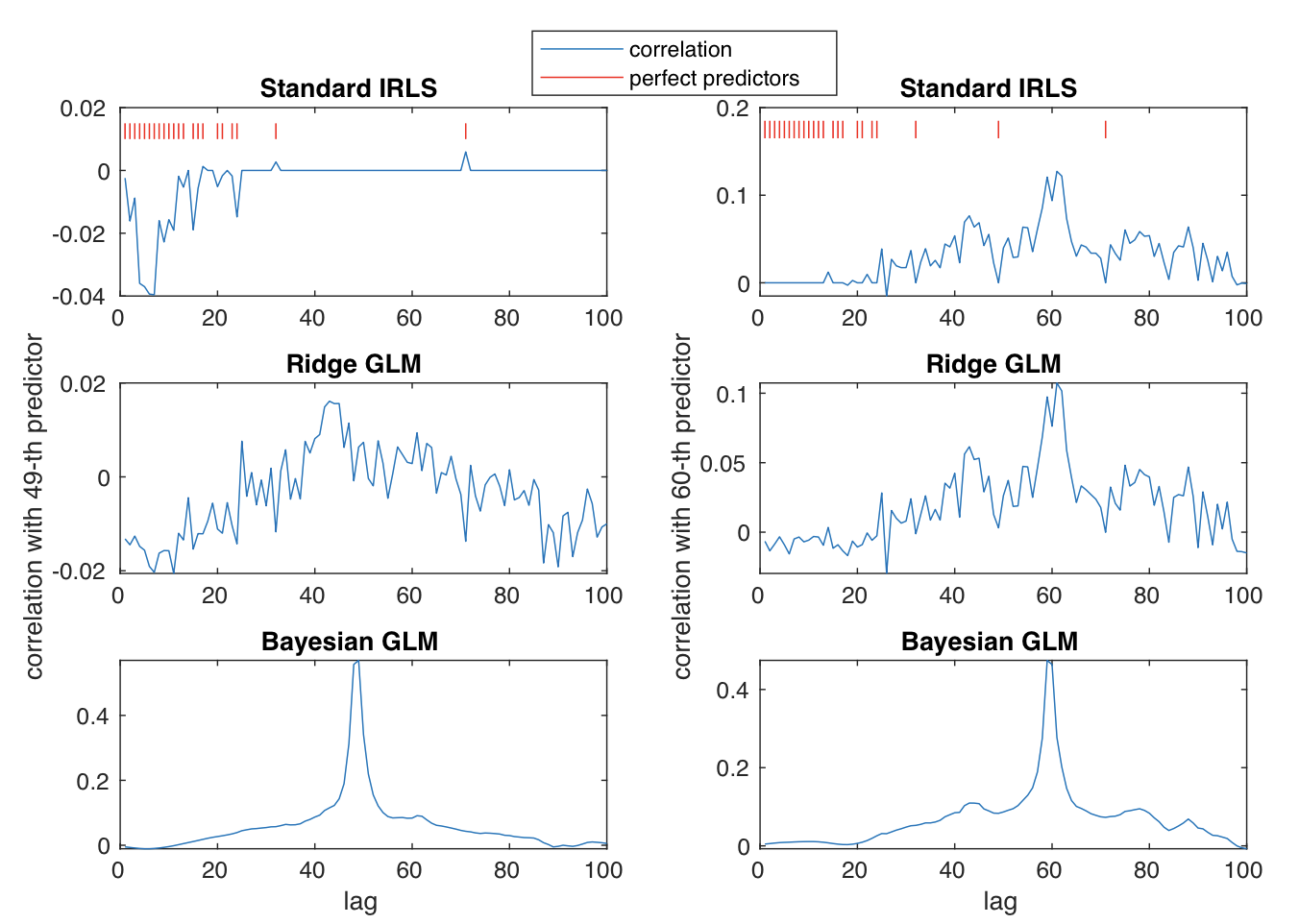
The Problem of Perfect Predictors in Statistical Analysis and How to Deal with it
The problem of separation arises when for some Generalized Linear Models (GLM) the IRLS algorithm fails to converge because the likelihood is maximized in the limit as one or multiple parameters tend to infinity. In this research project we explore a range of different approaches for dealing with this problem, compare them thoroughly, and end up with recommendations on which approach to be used under various circumstances.
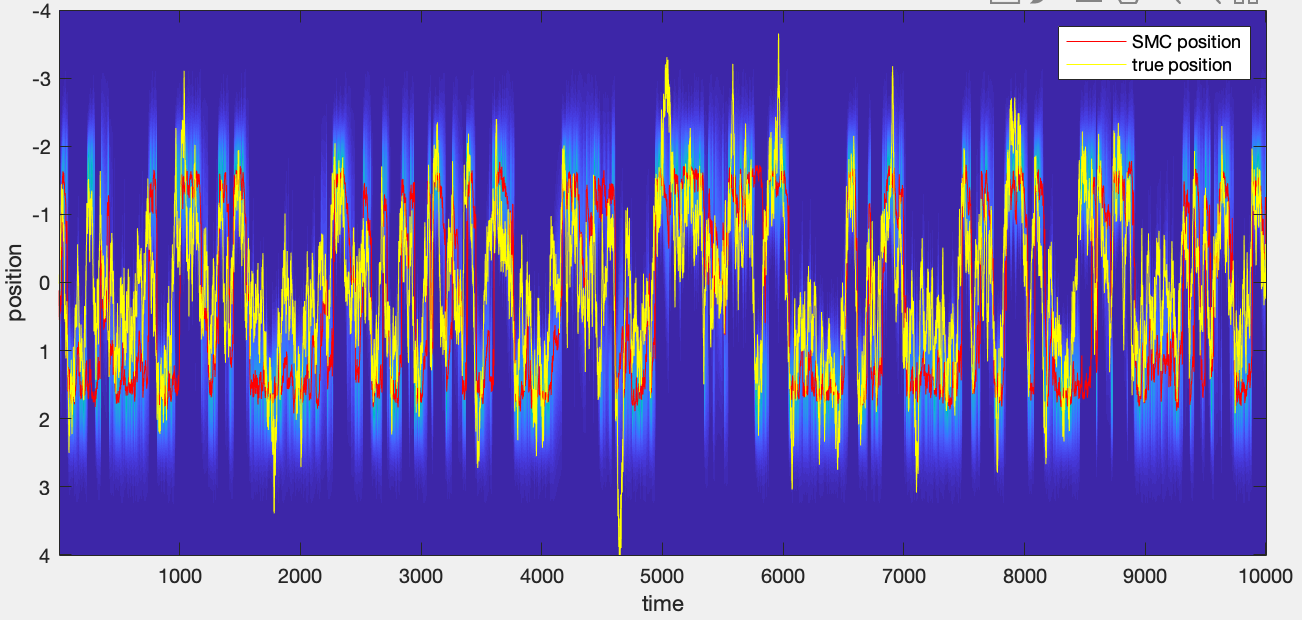
Clusterless Decoding of Position Using Marked Point Process in the Absence of Spike-sorting
Point process filters fail to successfully decode neural signals when spike sorting cannot be performed with high precision, e.g. in real time scnarios. An alternative approach for decoding neural signals is to use clusterless decoding. In this approach, a marked point process can be used to develop a statistical model that relates the covariate of interests, e.g. position of an animal, to features of the spike train.
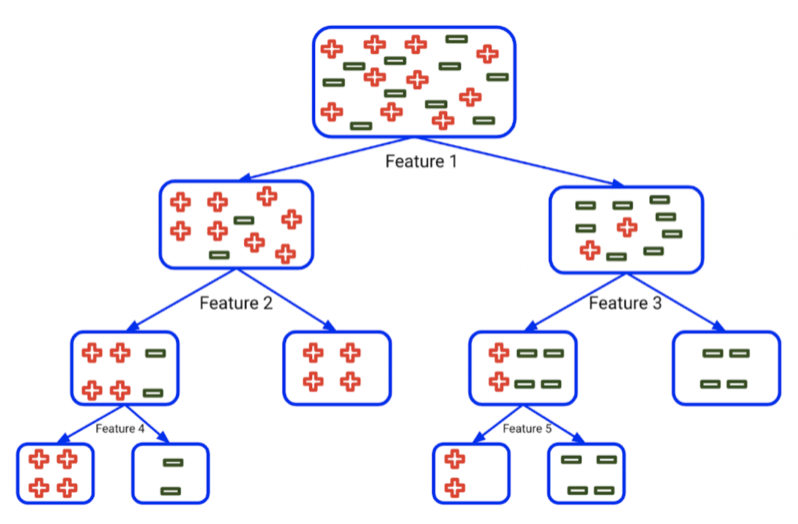
Random Forests Recommendation: When to Use?
In this project I discuss some advantages and disadvantages of random forests, and compare them to other methods such as SVM, Bagging, Adaptive Boost, relavance vector machine (RVM), LDA, and CART. I end up with recommendations on when other methods are likely to outperform random forests based on different properties of the data, such as sparsity, type of features, data size, and signal-to-noise ratio.
Approximation Algorithm for Maximum Distance of n Points
The problem of "finding the maximum distance between n points in an Euclidean space" has potentially many applications in different areas, e.g. in community detection algorithms, machine learning clustering, etc. The exact algorithm has the time complexity of O(n^2) which makes it infeasible for large data sets. I develop an approximation algorithm that solves this problem in "almost" linear time. For example, it returns an output with at most 1% error in O(4.5n).