Siu-Cheong Lau
MS
劉紹昌
Room 508, Department of Mathematics and Statistics,
Boston University
665 Commonwealth Ave, Boston, MA 02215
Email: 1lau1@math.bu.edu (remove the two 1’s)
About me
I am a faculty member in the Department of Mathematics and Statistics at Boston University.
Research interest
My main research interest lies in complex algebraic geometry and symplectic geometry, and more specifically mirror symmetry. With my dear collaborators, we developed mirror constructions via Lagrangian Floer theory that are closely related to homological mirror symmetry, the SYZ program, and the mirror maps.
More recently, I am particularly interested in group equivariance, quiver stacks formed by noncommutative deformations of Lagrangian immersions, and the interactions with sheaves and geometric representation theory.
I am excited about finding connections between quiver/stack/moduli/category theory and the relatively young subject of network models. Networks have provided important models and formulations of quantum physics. I hope it will help us to develop new and useful geometries, and perhaps reveal the true nature of our own spacetime in some day.
BKT workshop 2024 2023 2022
Art
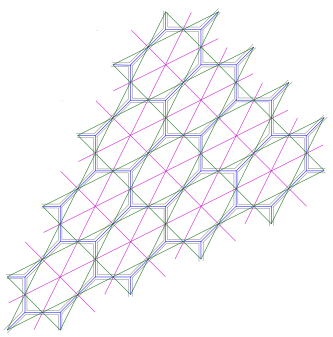
The above figure shows a hexagon tiling and some related graphs. It appears in the study of SYZ mirror symmetry, and is related to Riemann theta functions, modular forms, Gromov-Witten theory, and general-type varieties. It comes from my joint work with Atsushi Kanazawa.
The above figure shows several beautiful tessellations of the plane. Polygon countings in the figure have miraculous relations with periods of elliptic curves. It comes from my joint work with Cheol-Hyun Cho and Hansol Hong. In my joint work with Jie Zhou, we relate the countings with modular forms.
Publications
45. Mirror Construction for Nakajima Quiver Varieties, with Jiawei Hu and Ju Tan, arxiv:2404.16172.
44. Equivariant Lagrangian correspondence and a conjecture of Teleman, with Naichung Conan Leung and Yan Lung Li, arxiv:2312.13926.
43. Mirror Symmetry for Quiver Algebroid Stacks, with Junzheng Nan and Ju Tan, arxiv:2206.03028.
42. SYZ mirror symmetry for del Pezzo surfaces and affine structures, with Yu-Shen Lin and Tsung-Ju Lee, to appear in Advances in Mathematics, arxiv:2206.01681.
41. Disk potential functions for polygon spaces, with Yoosik Kim and Xiao Zheng, to appear in Journal of Symplectic Geometry, arxiv:2211.03558.
40. Quantum Finite Automata and Quiver Algebras, with George Jeffreys, Proceedings of MaxEnt 2022, arxiv:2203.07597.
39. Noncommutative Geometry of Computational Models and Uniformization for Framed Quiver Varieties, with George Jeffreys, Pure and Applied Mathematics Quarterly 19 (2023), no. 2, 731–789.
38. Kähler Geometry of Quiver Varieties and Machine Learning, with George Jeffreys, Foundations of Computational Mathematics 23 (2023), no. 5, 1899–1957.
37. Big Quantum cohomology of orbifold spheres, with Lino Amorim, Cheol-Hyun Cho and Hansol Hong, arxiv:2002.11180, to appear in Communications in Analysis and Geometry.
36. Equivariant SYZ mirror symmetry, to appear in ICCM proceedings 2019.
35. T-equivariant disc potentials for toric Calabi-Yau manifolds, with Hansol Hong, Yoosik Kim and Xiao Zheng, arXiv:1912.11455.
34. T-equivariant disc potential and SYZ mirror construction, with Yoosik Kim and Xiao Zheng, to appear in Advances in Mathematics, arXiv:1906.11749.
33. Immersed two-sphere and SYZ with applications to Grassmannians, with Hansol Hong and Yoosik Kim, Journal of Differential Geometry (2023), no. 3, 427-507.
32. On the Complex Affine Structures of SYZ Fibration of Del Pezzo Surfaces, with Tsung-Ju Lee and Yu-Shen Lin, Advances in Theoretical and Mathematical Physics Vol. 26, no. 4, 921-955, 2022.
31. Gluing Localized Mirror Functors, with Cheol-Hyun Cho and Hansol Hong, arXiv:1810.02045, to appear in Journal of Differential Geometry.
30. Affine elliptic surfaces with type-A singularities and orbi-conifolds, arXiv:1802.08891.
29. A note on disk counting in toric orbifolds, with Kwokwai Chan, Cheol-Hyun Cho, Naichung Conan Leung and Hsian-Hua Tseng, SIGMA 16 (2020), 055, 15 pages.
28. Open Gromov-Witten invariants and mirror maps for semi-Fano toric manifolds, with Kwokwai Chan, Naichung Leung and Hsian-Hua Tseng, Pure and Applied Mathematics Quarterly, Vol. 16, no. 3 (2020), 675-720.
27. SYZ mirror symmetry for hypertoric varieties, with Xiao Zheng, Communications in Mathematical Physics 373 (2020), no. 3, 1133–1166.
26. Mirror of Atiyah flop in symplectic geometry and stability conditions, with Yu-Wei Fan, Hansol Hong and Shing-Tung Yau, Advances in Theoretical and Mathematical Physics 22 (2018), no. 5.
25. Local Calabi-Yau manifolds of affine type A and open Yau-Zaslow formula via SYZ mirror symmetry, with Atsushi Kanazawa, Journal of Geometry and Physics 139 (2019), 103–138.
24. Geometric transitions and SYZ mirror symmetry, with Atsushi Kanazawa, arXiv:1503.03829, Pacific Journal of Mathematics, Vol. 301, no. 2, 2019.
23. Localized mirror functor constructed from a Lagrangian torus, with Cheol-Hyun Cho and Hansol Hong, Journal of Geometry and Physics 136 (2019), 284–320.
22. Noncommutative homological mirror functor, with Cheol-Hyun Cho and Hansol Hong, Memoirs of the AMS 271(2021), no.1326.
21. Moduli of Lagrangian immersions with formal deformations, Proceedings of the Gokova Geometry-Topology Conference 2017, 9-36, Int. Press, Somerville, MA, 2018.
20. Quantum corrections and wall-crossing via Lagrangian intersections, ICCM Notices.
19. Generalized SYZ mirror transformation, Proceedings of The 7th International Congress of Chinese Mathematicians, ALM 44, pp 139-153.
18. Lagrangian Floer potential of orbifold spheres, with Cheol-Hyun Cho, Hansol Hong and Sang-Hyun Kim, Advances in Mathematics 306 (2017), 344-426.
17. Localized mirror functor for Lagrangian immersions, and homological mirror symmetry for P^1_{a,b,c}, with Cheol-Hyun Cho and Hansol Hong, Journal of Differential Geometry 106 (2017), no. 1, 45-126.
16. Open Gromov-Witten invariants, mirror maps and Seidel representations for toric manifolds, with Kwokwai Chan, Naichung Conan Leung and Hsian-Hua Tseng, Duke Mathematical Journal 166 (2017), no. 8, 1405-1462.
15. Non-Kaehler SYZ mirror symmetry, with Li-Sheng Tseng and Shing-Tung Yau, Communications in Mathematical Physics 340 (2015), no.1, 145-170.
14. Modularity of open Gromov-Witten potentials of elliptic orbifolds, with Jie Zhou, Communications in Number Theory and Physics 9 (2015), no.2, 345-385.
13. Gross fibration, SYZ mirror symmetry, and open Gromov-Witten invariants for toric Calabi-Yau orbifolds, with Kwokwai Chan, Cheol-Hyun Cho and Hsian-Hua Tseng, Journal of Differential Geometry 103 (2016), no.2, 207-288.
12. Gross-Siebert's slab functions and open GW invariants for toric Calabi-Yau manifolds, Mathematical Research Letters 22 (2015), no.3, 881-898.
11. Genaralized SYZ and homological mirror symmetry, with Cheol-Hyun Cho,
Handbook for Mirror Symmetries of Calabi-Yau and Fano Manifolds.
-
10.Open Gromov-Witten invariants and SYZ under local conifold transitions, Journal of the London Mathematical Society (2) 90 (2014), no. 2, 413-435.
-
9.Toric, global, and generalized SYZ,International Congress of Chinese Mathematicians 2013.
-
8.Lagrangian Floer superpotentials and crepant resolutions for toric orbifolds, with Kwokwai Chan, Cheol-Hyun Cho and Hsian-Hua Tseng, Communications in Mathematical Physics 328 (2014), no. 1, 83-130.
-
7.Enumerative meaning of mirror maps for toric Calabi-Yau manifolds, with Kwokwai Chan, Naichung Conan Leung and Hsian-Hua Tseng, Advances in Mathematics 244 (2013), 605-625.
-
6.Open Gromov-Witten invariants and superpotentials for semi-Fano toric surfaces, with Kwokwai Chan, International Mathematics Research Notices (2014), no. 14, 3759-3789.
-
5.Open Gromov-Witten invariants on toric manifolds,
Oberwolfach Reports 9 (2012), no.2, 1265-1267. -
4.Mirror maps equal SYZ maps for toric Calabi-Yau surfaces, with Baosen Wu and Naichung Leung, Bulletin of the London Mathematical Society 44 (2012), no.2, 255-270.
-
3.A relation for Gromov-Witten invariants of local Calabi-Yau threefolds, with Baosen Wu and Naichung Leung, Mathematical Research Letters 18 (2011), pp. 943-956.
-
2.SYZ mirror symmetry for toric Calabi-Yau manifolds, with Kwokwai Chan and Naichung Leung, Journal of Differential Geometry 90 (2012), pp. 177-250.
-
1.Conformal geometry and special holonomy, with Naichung Leung, Recent Advances in Geometric Analysis 11 (2010), pp. 195-209.
Teaching (old and update stopped; I have switched to Blackboard)
Spring 2020, MA 822 Topics in Geometry (Quiver representations)
Fall 2019, MA 225 Multivariate Calculus
Fall 2019, MA 731 Lie Group
Spring 2019, MA 722 Differential Topology 2
Fall 2018, MA 225 Multivariate Calculus
Fall 2018, MA 563 Differential Geometry
Spring 2018, MA 731 Lie Group
Fall 2017, MA 563 Differential Geometry
Fall 2017, MA 123 Calculus 1
Spring 2017, MA 225 Calculus 3
Fall 2016, MA 725 Differential Geometry 1
Spring 2016, MA 722 Differential Topology 2
Spring 2016, MA 822 Topics in Geometry (Toric varieties and mirror symmetry)
......
Notes of selected talks
I hope you will find these notes helpful. Comments are welcome.
Quiver algebroid stacks and its applications
Mirror symmetry for quiver stacks with a view to machine learning
Equivariant disc potentials for SYZ torus fibrations
Moduli theory of Lagrangian immersions and mirror symmetry
A short trip to tropical geometry for high school students
Generalized SYZ and homological mirror symmetry
Awards
Best Paper Award (2019), ICCM
Best Paper Silver Award (2017), ICCM
Distinguished Paper Award (2017), ICCM
Certificate of Teaching Excellence (2014), Harvard University
Doctoral Thesis Gold Award (2012), New World Mathematics Award at ICCM
Hobbies besides mathematics
Chinese flute
Novels (金庸，古龍，黃易，三體...)
In the broad light of day mathematicians check their equations and their proofs, leaving no stone unturned in their search for rigour. But, at night, under the full moon, they dream, they float among the stars and wonder at the miracle of the heavens. They are inspired. Without dreams there is no art, no mathematics, no life.
Michael Atiyah