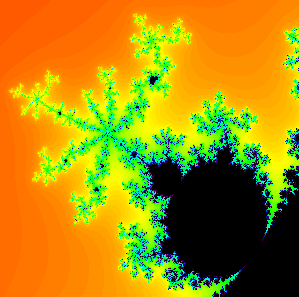
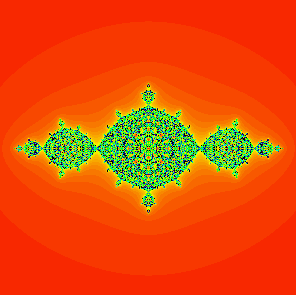
The 3/7-bulb hanging off the main cardioid in the Mandelbrot set. You can read off "3/7" by just looking at how the spokes are arranged in the antenna attached to this bulb. Or maybe you can just read this paper...

The 3/7-bulb hanging off the main cardioid in the Mandelbrot set. You can read off "3/7" by just looking at how the spokes are arranged in the antenna attached to this bulb. Or maybe you can just read this paper... |
This paper is a summary of a lecture I gave on the fractal
geometry of the Mandelbrot set at a conference at Mar-Athanasius College
in India. To appear in the Proceedings of the Seminar on Topology
and Fractals from that conference.
|
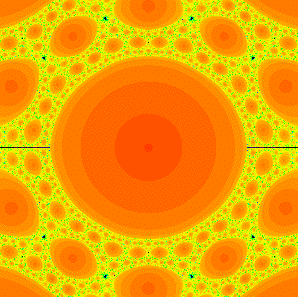
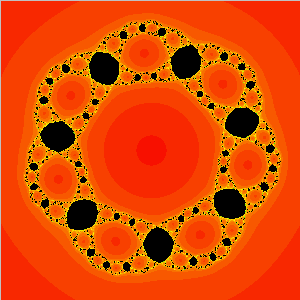
Mandelpinski necklaces surrounding the McMullen domain in the family z3 + C/z3. The red disks are Sierpinksi holes, and the black "dots" are really baby Mandelbrot sets. |
This paper is a survey of some recent results involving Mandelpinski
Necklaces for the family of rational maps zn +
C /zd. The main emphasis is on the case where n = d > 2, but the other cases are treated briefly. In Topological Dynamics and Topological Data Analysis, Springer (2021), 95-119.
|
The Sierpinski carpet, generated by playing the chaos game with eight vertices arranged at the ends and centers of the four sides of a square, with compression ratio 3 and no rotations. |
This paper is a pedagogical article aimed at showing high school teachers
how topics from dynamical systems can be incorporated into the curriculum
in order to get students excited about mathematics. Most of the paper
centers around the chaos game and its variants. In
Teaching and Learning Discrete Mathematics Worldwide:
Curriculum and Research, Springer ICME-13 Monographs (2018), 137-144.
|

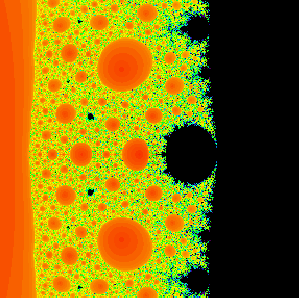
A different zoom into the Mandelpinski maze structure for the family of rational maps z2 + C / z3. The Mandelbrot sets are too small to be seen, but the red disks are Sierpinski holes. |
In this paper we give a survey of several different "Mandelpinski
structures" that arise in the families of rational maps
zn + C / zd where n, d > 1.
These structures include Mandelpinski necklaces, Mandelpinski spokes,
and a Mandelpinski maze. Ful details are provided in the papers below.
In Proceedings of the Oxtoby Centennial Conference, AMS
Contemporary Math Series 678 (2016), 133-150.
|
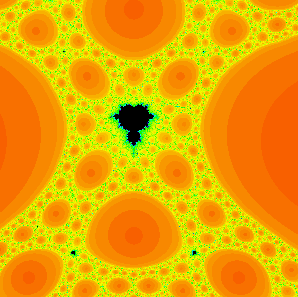
Some Mandelpinski spokes emanating from a baby Mandelbrot set in the parameter family of z2 + C / z3. The Mandelbrot sets are too small to be seen, but the red disks are Sierpinski holes. |
In this paper we describe another type of structure in the
parameter plane for rational maps of the form
zn + C / z d where n > 1 is even
and d > 2 is odd. These are Mandelpinski spokes.
Each spoke is an infinite collection of alternating Mandelbrot sets
and Sierpinski holes that extend away from certain Mandelbrot sets
in the Mandelpinski maze described in the following paper.
Journal of Difference Equations and Applications 22 (2016), 330-342.
|
A portion of the Mandelpinski maze along the negative real axis for z2 + C / z3. The Mandelbrot sets are too small to be seen, but the red disks are Sierpinski holes. |
In this paper we describe a new type of structure in the
parameter plane for rational maps of the form
zn + C / z d where n > 1 is even
and d > 2 is odd that we call a Mandelpinski maze.
The maze is an infinite collection of alternating Mandelbrot sets
and Sierpinski holes arranged along a complicated planar graph
with infinitely many vertices.
Indagationes Mathematicae 27 (2016), 1042-1058.
|
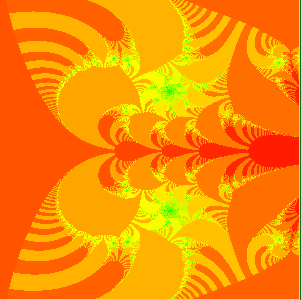
The Julia set for the complex exponential family C exp(z) when C > 1/e contains indecomposable continua. |
This paper is a brief overview of some of the interesting topological
spaces that arise as Julia sets for complex analytic maps. Included
are Cantor bouquets, indecomposable continua, and Sierpinski
curves. This is basically
an outline of a lecture given at a workshop on fractals at
the Rajagiri School of Engineering and Technology in Kochi, India in 2013
and at the conference on Geometry and Dynamics at the Lorentz Center
in Leiden, Netherlands in 2015.
Indagationes Mathematicae 27 (2016), 1116-1126.
|
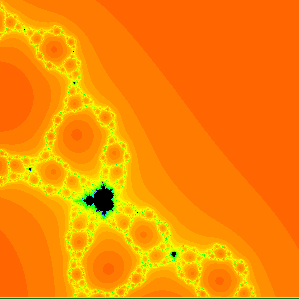
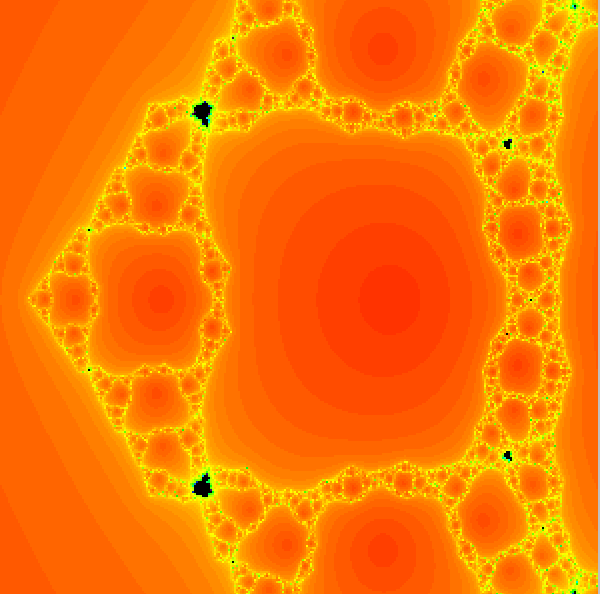
A magnification of the parameter plane for the family of maps z4 + C / z4 showing some accessible baby Mandelbrot sets. |
In this paper we prove that there exist infinitely many accessible
baby Mandelbrot set in the parameter plane for the family of rational maps
zn + C / zn where n > 1.
These are Mandelbrot sets
whose main cusp touches the exterior boundary of the connectedness
locus in the parameter plane. We also show that there is one such
Mandelbrot set for each external ray of angle j / nk - 1.
Qualitative Theory of Dynamical Systems 15 (2016), 49-66.
|
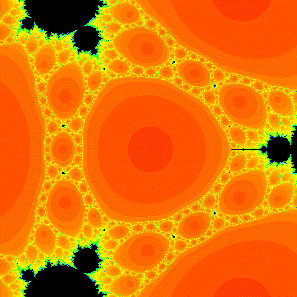
A magnification of the parameter plane for the family of maps z4 + C / z4 showing the Mandelpinski necklaces surrounding the central region which is the McMullen domain. |
In this paper we give a dynamical invariant for the Sierpinski
curve Julia sets that lie in the main cardioids of the baby Mandlebrot
sets attached to the Mandelpinski necklaces surrounding the
McMullen domain for the family
zn + C / zn when n > 2. This
invariant is basically the itinerary of the periodic critical orbit
as it winds through the various sectors bounded by Cantor necklaces.
Fundamenta Mathematicae 226
(2014), 253-277.
|

The parameter plane for the family of functions z2 + C / z2 showing the CMS tree with the main trunk along the horizontal axis. |
In this paper we construct what we call a Cantor-Mandelbrot-Sierpinski tree
in the parameter plane for the family of rational maps z2 +
c/z2. This is a "tree" whose trunk and infinitely many
branches are all Cantor necklaces. So most of the parameters in these regions
have Julia sets that are Sierpinski curves.
Meanwhile, between each pair of branches
there is also a baby Mandelbrot set extending outward from the main trunk of
the tree. Transactions of the AMS 366 (2014), 1095-1117.
|
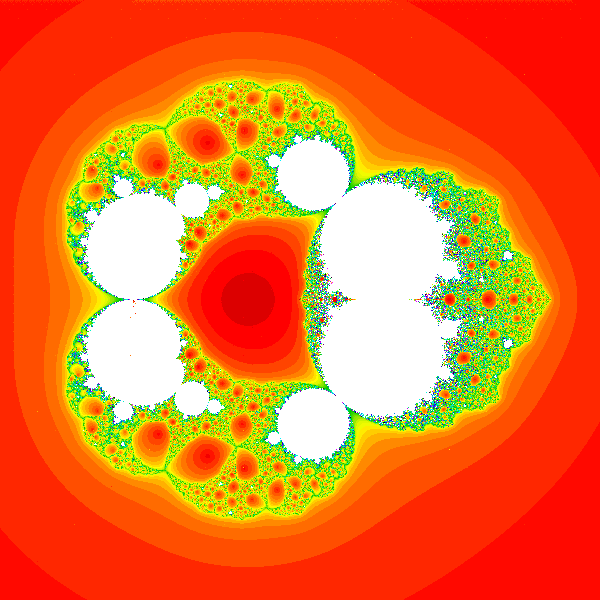
A slice of the parameter space for rational maps of degree 2. |
In this paper we give an almost complete set of conditions for a hyperbolic
rational map of degree two to have a Julia set that is a Sierpinski curve.
Annales Acadademiae Scientarum Fennicae 39 (2014), 3-22.
|

The Julia set corresponding to a singular perturbation of the Douady rabbit. |
In this paper we consider
maps of the form FA(z) = z2 + c + A /
z2 where c
is the center of a hyperbolic component in the Mandelbrot set. We prove that,
as A tends to 0, the Julia set of FA tends to the
FILLED Julia set of F0, i.e., the filled Julia set of the
simple quadratic function z2 + c. This generalizes the
result with Toni Garijo (below) where this was shown for c = 0 and
also the result with Mark Morabito (below) where maps of the form
zn + A/z were shown to have similar behavior, at leasst
when A approached the origin along n-1 straight
lines. Finally, in the paper A Generalized Version of the McMullen Domain
(also below), it was shown that this does not happen in the family
FA(z) = zn + c + A /
zn where c
is the center of a hyperbolic component of the Multibrot set and n > 2.
Ergodic Theory and Dynamical Systems 34 (2014), 171-184.
|

The McMullen domain for z3 + C / z3. This disk is surrounded by infinitely many Mandelpinski necklaces. |
This paper is a survey of much of the work that I have been
doing over the past few years involving the family of rational
maps zn + A/zd. Included are overviews
dealing with the escape trichotomy, Sierpinski curve Julia sets,
Mandelpinski necklaces, Cantor webs and necklaces, the crazy case
n = d = 2, more general singularly perturbed maps,
and a host of open problems. Bulletin of the American Math.
Society 50 (2013), 391-429.
|

A period 43 bulb off the main cardioid. How do you know this? Just count the spokes of the antenna hanging off the bulb. Can't count that high? See the paper below. |
This paper is a brief history of the past one hundred years in
the field of complex dynamics.
It also gives a brief introduction to such objects as Julia sets and the
Mandelbrot set. It is written to coincide with
the centennial of the Mathematical Association of America, which occurs in
2015. In A Century of Advancing Mathematics, MAA (2015), 15-34.
|
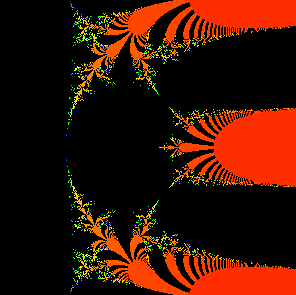
The main cardioid in the parameter plane for the family C exp(z). |
This paper is a brief overview of some structures in the parameter
planes for complex quadratic polynomials (the Mandelbrot set), singularly
perturbed rational maps, and the complex exponential. It is basically
an outline of a series of lectures given at a workshop on fractals at
the Rajagiri School of Engineering and Technology in Kochi, India in 2013.
In Fractals, Wavelets, and their Applications. Springer-Verlag (2014) 61-77.
|
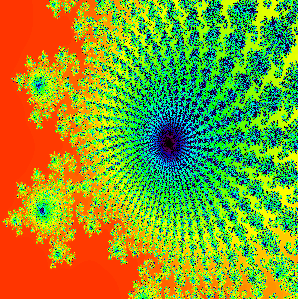
A magnification of the antennas in a period 43 bulb hanging off the main cardioid. How do you know this? Just count the spokes of the antenna hanging off the bulb. Maybe this is easier now than above. |
This paper is a brief survey of the structure of the principal bulbs
hanging off the main cardioid of the Mandelbrot set. Each of these bulbs
has its own "identity," and, as long as you know how to add and how
to count, you can identify each such bulb. Now I know many of you
think you know how to add, but this paper will convince you that
you are wrong! This is a summary of a lecture I gave at the Complex
Systems
Conference in Prague in 2013. and that will appear in the Proceedings of
that conference. In ISCS 2013: International Symposium on Complex
Systems. Springer-Verlag (2014) 3-8.
|

A Sierpinski carpet Julia set coresponding to the map z3 + (-.2 + 11i) / z3. |
This paper is just a brief, one-page note giving three reasons
why my favorite planar fractal is the Sierpinski carpet, not the triangle
(or gasket). Canadian Math Society Notes.
45 No. 3 (2013), 13.
|
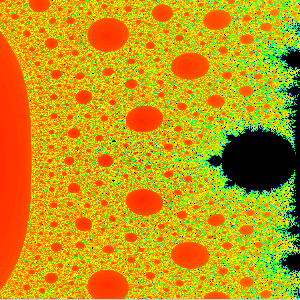
A magnification of the parameter plane for the family of maps z2 + C / z2. The Mandelpinski necklaces here are not as evident as they are in the case where n > 2. |
In this paper we return to the construction of Mandelpinski
necklaces that were proved to exist for the family of rational maps
zn + C / zn when n > 2
in several papers below. Here we extend these results to the very
different case n = 2. One main difference is that there
is no McMullen domain in this case, so the necklaces converge to
the origin in the parameter plane. Also, each of these special necklaces
only pass through one Mandelbrot set and one Sierpinski hole. When
n > 2, these necklaces pass through many more such sets.
In Difference Equations, Discrete Dynamical Systems and Applications.
Springer-Verlag (2016), 63-72.
|
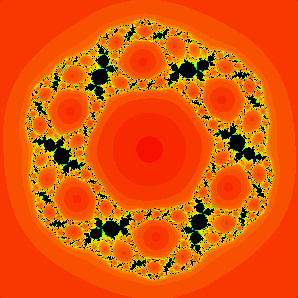
The connected Julia set for the map z3 + (.105 + .05i) / z2. Note the Douady rabbits that make up a portion of the Julia set for this map. |
This paper augments the results in the paper The Escape Trichotomy
for Singularly Perturbed Rational Maps (below).
We show here that, for the family
zn + C / zn, the Julia set is always a
connected set, except in two cases: the case where the Julia set is
a Cantor set and the case where it is a Cantor set of simple closed curves.
In Chaos, CNN, Memristors and Beyond, World
Scientific (2013), 239-245.
|
The Julia set for the map z2 -1 + A / z2. These Julia sets converge to the filled Julia set known as the basilica as A approaches 0. |
This paper is a survey of the different things that happen to the Julia sets
in the families
zn + c + A/zd as the parameter A
approaches 0 and c is at the center of a hyperbolic component
of the Multibrot set. When n = d = 2, we describe how the Julia sets
limit on the filled Julia set of z2 + c. Then we show that
this does not occur for most other cases. In Frontiers of
Complex Dynamics: In Celebration of John Milnor's 80th
Birthday. Princeton University Press (2014), 121-134.
|
A checkerboard Julia set corresponding to a map of the form z4 + C / z3. |
In this paper we describe the dynamics of maps of the form
maps of the form zn + C / zd where n >
1 and d > 0 and C is drawn from the main cardioid of one of
the
principal Mandelbrot sets in the parameter plane. These Julia sets (called
checkerboard Julia sets) are all homeomorphic but not all dynamically
equivalent. We prove that two such maps have conjugate dynamics if and only
if they have the same "minimal rotation number." In Int'l J.
Bifurcation & Chaos 23 (2013) 48-60.
|
The parameter plane for the family of maps z2 + C / z2. There is no McMullen domain around 0 when n = 2. |
In this paper we give three examples of how the dynamics of
maps of the form zn + C / zn are most
complicated when n = 2. There are three reasons for this. First,
there is no McMullen domain in this case, and secondly, because of this,
there are no
Mandelpinski necklaces surrounding the origin. Third, as C goes to
0, the Julia sets converge to the closed unit disk when n = 2, but this
does not occur for n > 2. In Conformal Dynamics and Hyperbolic
Geometry, Contemporary Math. AMS Vol. 573 (2012), 49-65.
|

The Julia set for the map z2 + .08 / z2. The extended rays for this map are all simple closed curves passing through 0 and infinity that meet the Julia set in a Cantor set. |
In this paper we give three examples of how external rays in the dynamical
plane may be extended completely through the Julia sets of certain rational
maps. These are maps of the form zn + C / zn.
In this case most of these extended rays are simple closed curves
passing through the origin (a pole) and infinity. They also
cut across the Julia set in a Cantor set of points. In certain cases,
these extended rays meet a critical orbit, in which case they bifurcate
into simple closed curves with (possibly infinitely many) attached
arcs. In Smale Festschrift, J. Fixed Point Theory and
Applications 7 2010, 223-240.
|
A baby Mandelbrot set in the family of degree 6 maps z3 + C / z3. |
In this paper we extend the concept of a dynamical plane external
ray to that of an internal ray. For a Cantor set of angles on the
unit circle, this is a curve that threads its way through the Julia set
of a map of the form zn + C/zn where
n > 2. Unlike external rays, all these internal rays
cross other internal rays at infinitely many points, and how
these crossings are arranged determine to a large part the
structure of the Julia set. In particular, these internal rays
allow us to prove the existence of (n-2)(2n-2)k-1
baby Mandelbrot sets of base period k in the parameter
plane for these families of rational maps. Fundamenta
Mathematicae 206 2009, 139-159.
|

The parameter plane for the family of degree 8 maps z4 + C / z4. |
This paper is a survey of many of the results in the papers
below dealing with singularly perturbed rational maps. We
concentrate for simplicity on the family
zn + c / zn where the parameter c
is complex. We describe the Escape Trichotomy Theorem, the classification
of escape time Sierpinski curve Julia sets, the structure around
the McMullen domain, Cantor necklaces, and Julia sets converging
to the unit disk. A subtheme in the paper is how the case
n = 2 is very different from the case n > 2.
In Nonlinear Dynamics and Chaos: Advances and Perspectives,
Springer-Verlag, Berlin, 2010, 13-29.
|

The Julia set for z3 - i + (-.025 + .034i) / z3 that is the center of a Sierpinski hole. Only the map with a complex conjugate parameter is conjugate to this one. |
In this paper, we consider families of maps of the form
zn + c/zn where the parameter c
is a center of a Sierpinski hole in the parameter plane. So
each of these Julia sets is homeomorphic to the Sierpinski carpet
and hence to each other.
We give a complete dynamic classification of these "escape time
Sierpinski curve maps," i.e., those maps for which the free
critical orbits escape. In particular, we show that there are
exactly (2n)k-3 different conjugacy classes
when n is odd and (2n)k-3 + 2k-4
classes when n is even. Here k is the escape time
of the critical orbits.
It is known that there are exactly (n-1) (2n)k-3
such centers of Sierpinski holes, so very few of these maps have
conjugate dynamics. The result holds for all maps in a Sierpinski hole,
not just for the centers. Fundamenta Mathematicae 202 (2009),
181-198.
|

The Julia set for z3 - i + A / z3 containing a Cantor set of decorated circles. |
In this paper, we consider families of maps of the form
zn + c +A/zn where the parameter A
is a center of a hyperbolic component of the Multibrot set and n > 2.
We show that, for c sufficiently small
the Julia set of this map contains a countable collection of
simple closed curves (some of which are "decorated") together
with an uncountable collection of point components. This generalizes a
result of McMullen which shows that, when A = 0, the Julia set is
a single Cantor set of simple closed curves. International
Journal of Bifurcation and Chaos 18 (2008), 2309-2318.
|

The parameter plane in the case n=5, showing in color the four dividing rays tending to the origin on which the Julia sets converge to the unit disk. |
In this paper, we consider families of maps of the form
zn + A/z where the parameter A
is drawn from n - 1 special dividing rays in the
parameter plane. We show that, as A approaches
the origin along these rays, the Julia sets converge as
a set to
the closed unit disk. This paper extends the results in
the paper below entitled
Julia Sets Converging to the Unit Disk. International
Journal of Bifurcation and Chaos 18 (2008), 3175-3181.
|
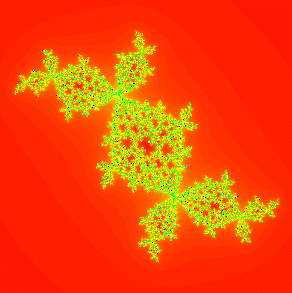
A singular perturbation of the Douady rabbit. The interior of each component of the filled Julia set of the rabbit contains a Sierpinski curve. |
In this paper, we consider families of maps of the form
z2 + c + A/z2 where c
is the center of a hyperbolic component of the Mandelbrot set
with period greater than 1 and A is a small complex
parameter. We show that, if |A| is sufficiently
small, then the Julia set of these maps are bounded on the
outside by a homeomorphic copy of the Julia set of z2
+ c. Also, assuming all of the critical orbits of the
map eventually enter the basin of infinity, then each internal
component of filled Julia set of this map is "wrapped" in
a set homeomorphic to the Sierpinski carpet. In
Complex Dynamics: Families and Friends, A. K. Peters (2009), 277-296.
|
The Mandelbrot set, or, as it is known in Arcadia, the "Coverly" set. |
Well, this is not really a research paper. Rather, it is a summary
of some of the mathematical ideas that arise in the wonderful play
by Tom Stoppard called Arcadia. Over the years, I have
been the "chaos consultant" for several theaters' production
of this play, and I find that people involved with this play
often want to learn a bit more about the mathematical ideas
involving chaos and fractals that swirl throughout the play. This paper
is an attempt to introduce these ideas at a relatively low level
and in a manner that is relevant to the various scenes in the play.
In The Beauty of Fractals: 6 Different Views, Mathematical
Association of America. Eds. Jon Scott and Dennis Gulick.
(2010).
|

The Julia set for F(z) = z2 -0.00001 / z2 is very close to the unit disk. |
In this paper we study the behavior of the Julia sets of the maps
Fc(z) = zn + c / zd where
n and d are both greater than or equal to 2
and c is small. When n = d = 2, we prove that the Julia sets
of these maps converge as c tends to 0
to the unit disk in the plane. But when one
of n or d is greater than 2, we show that there is
always an annulus of some fixed size that separates portions of the
Julia set. So the Julia sets do not converge to the unit disk in this case.
Proceedings of the American Mathematical Society 136 (2008), 981-988.
|
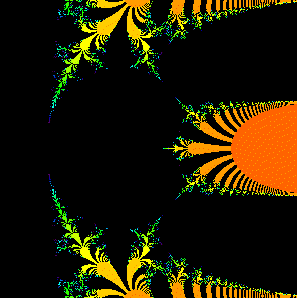
A portion of the bifurcation diagram (the analogue of the Mandelbrot set) for the complex exponential function C ez |
This paper is a survey of complex exponential dynamics. Topics covered
include preliminaries on complex dynamics,
Cantor bouquets, indecomposable continua, the parameter plane,
structural instability, the relation between the exponential and quadratic
(and other polynomial) dynamics, and some comparisons with other important
families of entire and meromorphic maps. In
Handbook of Dynamical Systems, Vol. 3. Eds. H. Broer, F. Takens, B. Hasselblatt. 2010, 125-224.
|

The McMullen domain for z3 + C / z3. The Cantor set of circles of Sierpinski curve Julia sets weaves its way in between the visible curves that contain collections of Sierpinski holes. |
In this paper we prove that, in the parameter plane for the family of maps
given by z3 + C /
z3, there is a Cantor set of simple closed curves on which each
parameter corresponds to a map whose Julia set is a Sierpinski curve. Hence
all these Julia sets are homeomorphic. However, only finitely many of these
maps are conjugate to another such map, so we have uncountably many
dynamically different maps on these curves. Related results are also proved
in the dynamical plane for the more general families zn + C /
zn where n > 2. Ergodic Theory and
Dynamical Systems 27 (2007), 1525-1539.
|
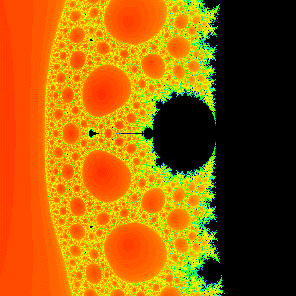
The McMullen domain when n=2, d=3. Actually, the domain is invisible in this picture since it is so small. It lies at the tip of the tail of the Mandelbrot set at the right. |
In this paper we consider families of maps of the form zn + C /
(z - a)d where a and C are complex and
|a| is not equal to one (and 1/n + 1/d < 1).
We are especially interested in the case where
a is close to 0. For when a = 0, there is a McMullen
domain in the parameter space, but as soon as a becomes nonzero, this
domain moves away from the origin and the Julia sets become very different. In
the McMullen domain, the Julia sets are Cantor sets of concentric circles
about the origin; when a is nonzero, the Julia set consists of
infinitely many circles, only one of which surrounds the others, and
uncountably many point components. Topology Proceedings 32 (2008),
301-320.
|
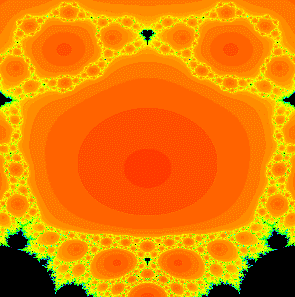
A portion of the parameter plane for z3 + c / z3 showing a Cantor 4-web. The web is the union of many of the open regions plus a Cantor set of points. |
In this paper we prove that there is a "Cantor 2n-2-web" in both the
dynamical and the parameter plane for complex rational maps of the form
zn + C / zn. Roughly speaking, a Cantor k-web
consists of an open disk which is surrounded by k smaller open disks. Then
each of these disks are surrounded by k smaller open disks. And so
forth. Finally, this sturcture is joined together by adding a Cantor set of
points that makes the entire set connected. In the dynamical plane, the
dynamics of the map on each of these sets is always the same: on the Cantor
set portion of the web, the map is conjugate to the shift map, while points
in the open disks eventually escape to infinity. This structure occurs for
all parameters c for which the Julia set is connected.
Fields Institute Communications 53 (2008), 105-123.
|
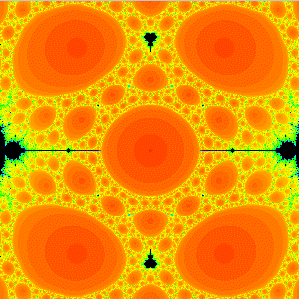
A magnification of the McMullen domain in the parameter space for the family of rational maps z3 + A / z3. Note the "circles" meeting 4, then 10, then 28 Sierpinski holes surrounding the central McMullen domain. |
In this paper we prove that the kth
ring around the McMullen domain
(as described in the paper below) for the family of rational
maps zn + C / zn
when n > 2 is the home of precisely
(n - 2)nk-1 + 1
parameters that are centers of baby Mandelbrot sets of base period k.
and the same number of parameter values that are centers of Sierpinski holes
with escape time k+2. We also show that these Sierpinski holes are
always homeomorphic to disks and that there is a unique parameter in each
hole for which the critical orbit lands on infinity at iteration k+2.
Finally, we show that there are exactly (2n)k-3(n-1)
Sierpinski holes in the parameter plane with escape time k. These last
two results are straightforward generalizations of results
of Pascale Roesch, who proved these facts in the
case n = 2. Conformal Geometry and Dynamics 11 (2007), 164-190.
|

A magnification of the McMullen domain in the parameter space for the family of rational maps z4 + A / z4. |
In this paper we prove that the McMullen domain for the family of rational
maps zn + C / zn
when n > 2 is surrounded by infinitely many disjoint simple closed
curves Ck converging down to the boundary of the domain as
k tends to infinity. On Ck, there are precisely
parameters that are superstable (i.e., for which a critical orbit is periodic), and the same number of parameter values for which the critical orbits land on the pole at 0 (i.e., parameters that are centers of Sierpinski holes). Transactions of the American Mathematical Society 359 (2007), 3251-3273.
|

The explosion that produces indecomposable continua in the family C exp(z) when C increases through 1 / e. |
In this paper we give a survey of some open problems that occur on the
"boundary" of complex dynamics and topology. Included are problems dealing
with indecomposable continua and Sierpinski curve Julia sets that arise in
complex dynamical systems. In Open Problems in Topology II, ed. Elliott Pearl,
Elsevier (2007), 469-478.
|
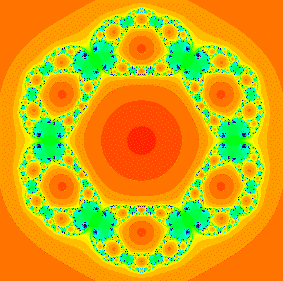
A Julia set for a singularly perturbed function of the form z3 + C / z3. |
In this paper we give a survey (with some proofs in elementary cases) of the
vast
array of different phenomena that occur in the family of rational maps
|
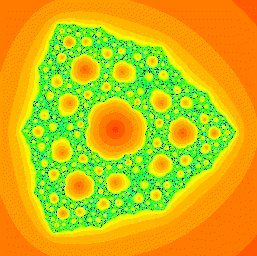
An example of a structurally unstable Sierpinski curve Julia set from the family of functions z2 + C / z. |
In this paper we show that the family of maps FA(z) = zn + A
z-n with n > 1 admits infinitely many parameter values
A for which
the Julia set is a Sierpinski curve that is structurally unstable in the sense
that, arbitrarily close to A, there are infinitely many parameter
values for which:
|

A Sierpinski curve Julia set for the function z3 + 0.13i / z3. |
In this paper we survey the many different ways that Sierpinski curves can
appear as the Julia set of a member of the family of rational maps of the form
zn + C / zd . In Difference Equations,
Special Functions, and Orthogonal Polynomials. World Scientific (2007), 131-148.
|

The Julia set for the function
|
In this paper we construct models for certain Julia sets in the
families of rational maps z2 + A / z2 and
z2 + B / z. These Julia sets are generalized
Sierpinski gaskets and are produced when the critical orbits for these
maps land on repelling periodic points in the boundary of the
basin of infinity. We
also show that, excluding a certain symmetry, no two of these Julia
sets are homeomorphic. Topology and its Applications 154 (2007), 11-27.
|
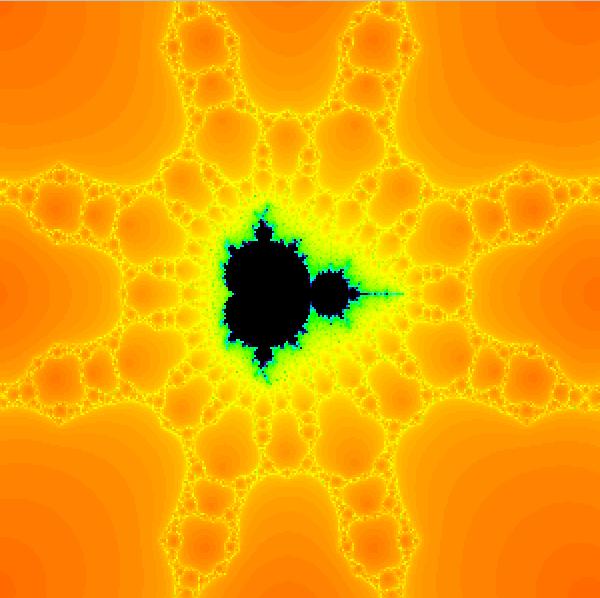
The Mandelbrot set. |
This paper is an elementary description of the Mandelbrot and Julia sets written for students who are familiar with complex numbers. Online in Plus Magazine, 2006.
|

The parameter plane for the family
|
In this paper we describe the structure of the parameter plane for the family of
rational maps given by
C(z + 1 / z). We show that in any neighborhood of C=0 there
are infinitely many parameters for which the Julia set is the entire plane
(blowup parameters) as well as infinitely many copies of small Mandelbrot
sets. In
Complex Dynamics: Twenty-Five Years After the Appearance of the Mandelbrot
Set, American Mathematical Society, Contemporary Math, 396, 2006,
51-62.
|

A baby Mandelbrot set in the parameter space for z3 + C / z3. Note the red regions attached to the endpoints of certain antennas in this Mandelbrot set --- these are the "halos." |
In this paper we prove the existence of "principal" Mandelbrot sets in the
parameter planes for the functions zn + C / zn
when n > 2. We also show that each of these Mandelbrot sets has
infinitely
many halos attached. These halos are Sierpinski holes in which the
corresponding maps have Julia sets that are Sierpinski curves. The halos are
attached at the endpoints of the antennas of the Mandelbrot set corresponding
to Misiurewicz parameters where (in the quadratic polynomial case) the external
rays of argument p/2k would land.
In Complex Dynamics: Twenty-Five Years After the Appearance of the
Mandelbrot Set, American Mathematical Society. Contemporary Math, 396, 2006,
37-50.
|

The parameter plane for the family of functions z2 + C / z2. |
In this paper we give a survey of the dynamical and parameter planes for the
family of rational maps
Fc(z) = z2 + c/z2.
In Dynamics on the Riemann Sphere, ed., P. Horth and C. Petersen. European Math Society, 2006, 97-119.
|

A Sierpinski curve Julia set for the function z2 -1 / 16 z2. |
In this paper we prove that, for the family of rational maps
|

The parameter space for the family of rational maps z3 + A / z3. The central hole in this image is the McMullen domain. |
In this paper we prove that the McMullen domain for the family of rational
maps zn + C / zn
when n > 2 is a single simply connected open subset of the parameter
plane.
We also show that this domain is bounded by a simple closed curve. Here the
McMullen domain consists of those parameter values for which the Julia set is
a Cantor set of simple closed curves. Fundamenta Mathematicae. 185
(2005), 267-285.
|

A Julia set for a complex exponential function. |
In this paper we describe several new types of invariant sets that appear in
the Julia sets of the complex exponential function c ez.
These sets include indecomposable continua formed by a pair of hairs that
accumulate upon one another, and also another indecomposable continuum which
is the set of accumulation points of a completely separate hair.
International Journal of Bifurcation and Chaos 15 (2005),
3281-3293.
|
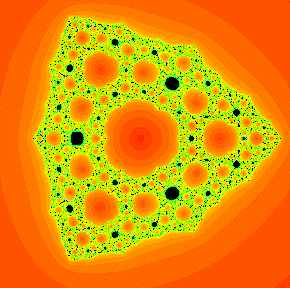
A buried Sierpinski curve Julia set for the function z2 -0.328 / z. |
In this paper we prove the existence of a different kind of Sierpinski curve
Julia set from the ones described in earlier papers. These Sierpinski curves
have complementary domains that consist not only of the basin of attraction of
infinity, but also of the basins of other finite attracting cycles. Discrete
and Continuous Dynamical Systems. 13 (2005), 1035-1046.
|

Another example of a Sierpinski curve Julia set, this time from the family
|
In this paper we describe a family of rational maps of the complex
plane that feature infinitely many distinct parameter values for which
the corresponding Julia set is a Sierpinski curve (sometimes called a
Sierpinski carpet). Although all of
these Julia sets are homeomorphic, we prove that there are infinitely
many open sets in the parameter plane in which the corresponding maps
on the Sierpinski curve have different (non-conjugate) dynamics.
Ergodic Theory and Dynamical Systems 25 (2005),
1047-1055.
|

An example of a Julia set that is a Cantor set of Jordan curves. The map here
is
|
In this paper we discuss a trichotomy that occurs in the topology of
the Julia sets of rational maps of the form zn + A /
zd. We show that, depending upon how the critical
orbit escapes to
infinity, the Julia set is either a Cantor set, a Sierpinski curve, or
a Cantor set of circles. Indiana University Mathematics
Journal 54 (2005), 1621-1634.
|

Another example of a Sierpinski curve Julia set also drawn from the family
|
In this paper we describe the dynamics of a particular member of the
family of rational maps of the complex plane given by F(z) =
z2 + c / z2 .
For this family there are infinitely many distinct parameter values for which
the corresponding Julia set is a Sierpinski curve (sometimes called a
Sierpinski carpet). Using symbolic dynamics, we analyze completely the
case where c = -1/16. This is the typical case in this family;
the dynamics on all other Julia sets may be handled in similar
fashion. Journal of Difference Equations and
Applications. 11 (2005), 581-596.
|

Yet another Sierpinski curve Julia set drawn from the family of functions z2 + C / z2. |
In this paper we describe several examples of interesting topological
spaces (Sierpinski curves, Cantor bouquets, and indecomposable
continua) that also arise as the Julia sets of complex functions.
Notices of the American Mathematical Society. 51 (2004), 9-15.
Color Figures: |
This paper surveys some of the surprising changes in the topological structure of Julia sets for entire functions that occur when parameters are varied. Topology Proceedings. 28 (2004), 99-112.
This paper is a survey paper written for high school teachers and describing the results of various chaos games. Mathematics Teacher. 98 (2004), 228-233.
In this paper we describe the global bifurcations in the family F(z) = z2 + c/z, i.e., the singular pertubation of z2 obtained by adding a pole at the origin. International Journal of Bifurcation and Chaos 14 (2004), 161-169.
In this paper we discuss an interesting phenomenon in the exponential family where certain exponential functions have orbits that can "catch up" with other, supposedly faster orbits. The American Mathematical Monthly 111 (2004), 704-708.
In this paper we review several interesting dynamical and topological constructions dealing with the complex exponential function K ez where K > 0. In: New Progress in Difference Equations, ed. B. Aulbach, S. Elaydi, and G. Ladas. Chapman & Hall/CRC (2004), 105-122.
This is a summary of a lecture that was presented at Short Course on Symbolic Dynamics and Its Applications held at the joint AMS-MAA meeting in San Diego in January, 2002. In Symbolic Dynamics and its Applications, Proceedings of the Symposia in Applied Mathematics 60 (2004), 37-60.
We describe a family of semilinear maps of a strip in the plane, each of which features an invariant indecomposable continuum. The dynamics on and topology of these continua resemble those of the complex exponetial family Ek(z) = cez. In Topology Proceedings 26 (2002), 153-167.
We show that there are many itineraries for the complex exponential map for which the corresponding set of points is an indecomposable continuum, not a hair, as occurs in the case of bounded regular sequences. The itineraries for which this occurs include bounded sequences which consist of longer and longer blocks of zeroes, the length of which grows quickly. Conformal Geometry and Dynamics 6 (2002), 1-12.
We describe the hyperbolic components of the parameter plane for the complex exponential family using two tools: a parameter plane kneading sequence and a dynamical plane kneading sequence. We prove the existence of a hyperbolic component with any parameter plane kneading sequence and investigate the relationship between these two sequences. In Fundamenta Mathematicae 174 (2002), 193-215.
This paper proves that one can determine (using harmonic measure) the p/q bulb in the Mandelbrot set by looking at the geometry of its antenna. Fractals. 10 (2002), 39-46.
We discuss which points in the Julia set of a complex exponential map are accessible from the basin of attraction of an attracting cycle. Basically, only certain of the endpoints of hairs in this Cantor bouquet are accessible. Those endpoints that are accesssible are determined by the kneading sequence of the map. Discrete and Continuous Dynamical Systems. 1 (2001), 299-318.
We prove that a saddle-node (parabolic) periodic point in a complex dynamical system often admits homoclinic points, and in the case that these homoclinic points are nondegenerate, this is accompanied by the existence of infinitely many baby Mandelbrot sets converging to the saddle-node parameter value in the corresponding parameter plane. In Global Analysis of Dynamical Systems, ed.: H. Broer, B. Krauskopf, G. Vegter. IOP Publishing (2001), 329-338.
In this paper we discuss the kneading sequence for complex exponential maps and show how this sequence can be used to determine how many hairs are tied together in the Julia sets of these maps. Ergodic Theory and Dynamical Systems 20 (2000), 1603-1617.
This paper investigates how the parameter plane for the degree d polynomial family C(1 + x/d)d is related to the corresponding plane for the exponential family Cez. Journal of Difference Equations and Applications 6 (2000), 275-307.
In this paper we prove the existence of invariant curves or "hairs" that lie in the Julia set of the complex exponential family EK(z) = Kez. We also discuss similar curves that lie in the parameter plane for this family. On these curves, the Julia set of the corresponding exponential is the entire complex plane. International Journal of Bifurcation and Chaos. 9 (1999), 1517-1534.
This paper investigates several interesting aspects of the topology of the Julia set of the complex exponential family. Publicacions Matematiques. 43 (1999), 27-54.
This paper discusses and makes precise several of the "folk theorems" regarding the size of various portions of the Mandelbrot set. American Mathematical Monthly 106 (1999), 289-302.